※本グラフPgmの基礎は、Bitmap展開のシリーズで解説してあります。全計測データを巨大なBITMAPに展開して、切り取り、拡大する方式です。
GPSドップラーデータ生データは、ノイズが多くて、平滑済みのF9Pのデータと比較できないので
M9Nの25Hzドップラーデータをローパスフィルタで馴らしてみました。
ノイズFFTでは、サンプリング25Hzと2Hz以下でピークがある
ドップラーのノイズに関しては、論文がありました。やはり相当ノイズをかぶってました。
豊田中研2012「GPSドップラと慣性センサの統合による車両軌跡推定手法の提案」
東京海洋大学の「GPSによる測定値と誤差要因」プレゼン資料
https://www.denshi.e.kaiyodai.ac.jp/kubo/chapter5_kubo.pdf
●ローパスフィルター参考にさせていただいたPgm
簡単で分かりやすいものを探したら、ExcelVBAで作ってある
EasyLowpassというフリーソフトがvectorに掲載されていました。
https://www.vector.co.jp/soft/winnt/business/se443007.html
バターワースフィルターは、基本的なフィルタで解説は、WIKIが分かり易いです。
https://ja.wikipedia.org/wiki/%E3%83%90%E3%82%BF%E3%83%BC%E3%83%AF%E3%83%BC%E3%82%B9%E3%83%95%E3%82%A3%E3%83%AB%E3%82%BF
Bryantについては、参考文献がみつかりませんでした。
●Easy lawpass様の解説も丁寧で、プログラムもシンプルなので、これをC#へ移植してから、少し改造しました。
VBAのプログラムの関数部分
| ‘2次元配列に対してBryantのローパスフィルタをかける関数の改変バージョン
‘入力配列と出力配列が別個に存在,入力配列を書き換えない ””””’BryntFilter (入力2次元配列,出力2次元配列,開始行,終了行,開始列,終了列,カットオフ周波数,計測周波数) Public Sub BryantFilter2(ByRef f() As Double, ByRef fout() As Double, rowmin As Integer, rowmax As Integer, colmin As Integer, colmax As Integer, fc As Double, fs As Double) ‘配列rowmin行目からrowmax行まで,colmin列目からcolmax列までを平滑化する Dim i As Integer Dim j As Integer ReDim temp(rowmax, colmax) As Double For i = rowmin To rowmax: For j = colmin To colmax temp(i, j) = f(i, j) fout(i, j) = f(i, j) Next j: Next i: ‘Bryant のバターワースフィルタ,臨床歩行分析入門より Dim FF As Double Dim W As Double Dim B As Double Dim c As Double Dim D As Double FF = fc / fs W = Tan(3.14159 * FF) B = 1 + Math.Sqr(2) * W + W * W c = 2 * (1 – W * W) / B D = -(1 – Math.Sqr(2) * W + W * W) / B For j = colmin To colmax For i = rowmin + 2 To rowmax fout(i, j) = (temp(i, j) + 2 * temp(i – 1, j) + temp(i – 2, j)) * W ^ 2 / B + c * fout(i – 1, j) + D * fout(i – 2, j) Next i Next j
‘反対側からもう一度 For i = rowmin To rowmax: For j = colmin To colmax temp(i, j) = fout(i, j) Next j: Next i: For j = colmin To colmax For i = rowmax – 2 To rowmin Step -1 fout(i, j) = (temp(i, j) + 2 * temp(i + 1, j) + temp(i + 2, j)) * W ^ 2 / B + c * fout(i + 1, j) + D * fout(i + 2, j) Next i Next j End Sub |
このプログラムを複数データ列を一挙に計算するために、2次元配列になってますが、C#では、1列のデータを
フィルター処理する方法に改造しました。短いので、なんとか動作しました。
元データをf[]で渡して、出力をfout[]で受け取る関数です。計算方向を正逆しているので、遅延がなくなってます
| //======================================================================================= //=======================Low Pass Filter================================================= //======================================================================================= //private void BryantFilter2(double[,] f,double [,]fout, int rowmin, int rowmax, int colmin, int colmax, double fc, double fs) private void BryantFilter2(double[] f, double []fout, int rowmin, int rowmax, int colmin, int colmax, double fc, double fs) { int i, j; double[] temp = new double[rowmax];for(i=rowmin;i<rowmax;i++) { for (j = colmin; j <= colmax; j++) { temp[i] = f[i]; fout[i] = f[i]; // Debug.Print(“temp[” + i.ToString() + “,0]=” + temp[i, 0].ToString()); } } //Bryant のバターワースフィルタ,臨床歩行分析入門より double FF,W,B,c,D;FF = fc / fs; W = Math.Tan(3.14159 * FF); B = 1 + Math.Sqrt(2) * W + W * W; c = 2 * (1 – W * W) / B; D = -(1 – Math.Sqrt(2) * W + W * W) / B;j =0; for (i = rowmin + 2; i < rowmax-1; i ++) { fout[i] = (temp[i] + 2 * temp[i – 1] + temp[i – 2]) * W *W / B + c * fout[i – 1] + D * fout[i – 2]; // Debug.Print(“InFilter:temp[“+i.ToString()+”,”+j.ToString()+”]=” + temp[i].ToString() + “,fout[“+i.ToString()+”]=” + fout[i].ToString()); }Debug.Print(“Pass1″+”rowmax=”+rowmax.ToString()); //反対側からもう一度 for (i = rowmin; i < rowmax; i++) { j = 0; temp[i] = fout[i];}for( i = rowmax -3;i> rowmin;i–) { fout[i] = (temp[i] + 2 * temp[i + 1] + temp[i + 2]) * W * W / B + c * fout[i + 1] + D * fout[i + 2]; fkekka[i] = fout[i]; // Debug.Print(“GyakunFilter:temp[” + i.ToString()+ “]=” + temp[i].ToString() + “,fout[]=” + fout[i].ToString(), “fkekka=” + fkekka[i].ToString()); }}// BryantFileter END================================================================= |
全体の解析プログラムのソース備忘録
https://gist.github.com/dj1711572002/6356c9c6a6233fc35e1ae7de1e3a22be
●計算結果
①M9NのgSpeedが最もノイズをかぶっていたのですが、2Hzでカットするときれいになってます。
②さらに平滑化して1HzでカットオフするとF9Pより滑らかになりました。この波形は、自転車の蛇行運転している最中ですので、動作は1Hz以下ですので、M9Nの波形のほうが実際に近いと思います。
=>ハンドルにエンコーダをつけて、比較してみれば、もっと正確にフィルターの比較ができます。
赤がF9PのgSpeed、水色がM9NのgSpeedのFilter済み 6500mm/sec=23km/h
ピンクF9PのvelN、黄色M9NのvelN Filter済み、波形としては、M9Nがきれいです。F9Pはいびつ形状
緑F9PのvelE、青M9NのvelE Filter済み、velN同様にM9N波形がF9Pよりきれいです。
F9Pは、10Hzなのでがたがた気味です。
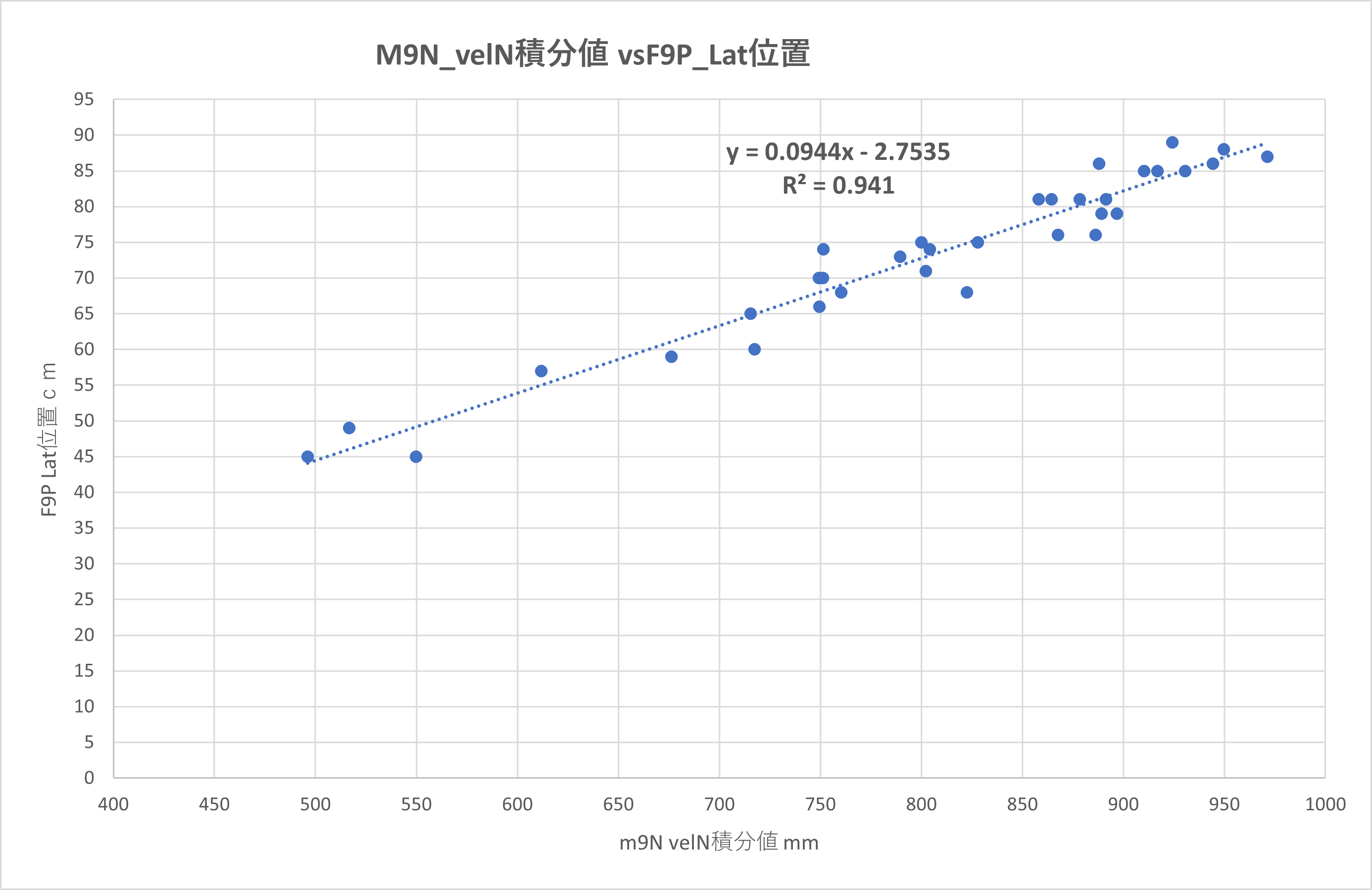
③波形がきれいなので、M9NのvelNの積分値とF9Pの測位値Latの位置を比較してみました。
直線性はある程度でてますが。誤差で±5cm 幅で10cm程度誤差がでる結果です。
フィルター無しのデータの積分の場合50cm~1m程度誤差がでていたので、ローパスの効果大でした。
M9Nの測位実力が1mですが、積分値だと10cm精度まで出ることが判りました。
長時間だと大きな誤差がでますが、200msec周期以内なら10cm精度がでることが判りました。
F9Pの補間としては、10cmで使えるか速度と曲率の条件で考えていきます。
計算のEXCEL備忘録で置いておきます。dgv_SkyRoad_airbone4g_02_1hz
④時間軸を10倍にして拡大波形をみると
1秒間にわたって、大きくF9PとM9Nの波形がずれている部分がみつかりました。
速度で、600msec/hで方向で5度差ですので、大きな位置差が発生します。
F9PとM9Nのどちらが正しいのか、別のセンサで自転車の蛇行を測定しないと白黒がつきませんので
ハンドルの回転角センサをとりつける検討をはじめます。