２０２５年のSTA計測は、プロ級の方がテストライダーをしていただけます。
プロ級の方のターンの見方と感覚をお聞きして、何がポイントになるのか、勉強させていただいてます。小賀坂スキーの横田様からスラローム競技のターンの基礎知識の教材として論文をいただきました。

●片側スキーだけで良いので助かった。
STA22,23,24とデバイスとシステムの開発で要素は大夫そろったのですが、実際のフィールド計測を
どうやっていくから、レイアウトとか実装は自分がライダーだと決められなかったのですが、今回横田様というスキー滑走もプロ級のスキー設計のエンジニア様からアドバイス得られて助かりました。
いろいろ、お話しをきくと、スキー板の評価とターンの分析なら、片側スキー一本で計測すれば事足りるとのことでした。片側だけでいいなら、開発工数が半分近くになりますので、非常に助かります。
私一人でSTAを使う場合は、両足の同程度のデータが必要で、自分の下手な滑りがどうなっているのかみるには、両足が必要なのですが、プロ級の方からすればターンは完璧に調整できるので、片側だけの情報があれば全てわかるというのは、なるほどと感じました。

●スラロームスキーの論文
基本的なことをきちんと網羅されているので、初学者には、ちょうどよい論文をいただきました。

Alpine Ski Motion Characteristics in Slalom
https://www.frontiersin.org/journals/sports-and-active-living/articles/10.3389/fspor.2020.00025/full

中程度の急勾配（ 19° ）のスラロームターンでは、スキーエッジ 角は 10mと 13mのゲート間隔で 65.7±1.7° と 71.0±1.9° の最大値に達した。旋回半径は 10mコースで 3.96± 0.23m、 13mコースで 4.94± 0.59mが最小値とな りました 。これらの値は， Howe (2001)によるエッジ 角に基づく旋回半径の理論的予測とよく一致していました。 また、スキーの幾何学的特性と物理的特性がスキーの軌道を決定するためにどのように相互作用しているのか、特に低エッジ角でのスキーの軌道を決定するためにどのように相互作用しているのか、さらなる研究の必要性を指摘しています。

スキーの特性がスキーと雪の相互作用にどのような影響を与えるかについての理解を深めるために、本研究の目的は、スラロームレースのシミュレーション中に高度なスキルを持つスキーヤーから収集した 3次元運動学的データセットを使用してスキーの運動特性を定量化し、これらの測定値を理論的な予測値と比較することでし

●概要
１：今までの知見

１－１：〜 アルペンスキーの特徴〜
 アル ペンスキーは、雪面との相互作用に影響を与える幾何学的・物理的特性を持っています。サイドカットと呼ばれる滑らかでカーブしたエッジプロファイルを持ち、その量はスキーの種類によって異なります。スキーのサイドカットを記述するために 2 つのパラメータが使用されます： サイドキャンバーとサイドカット半径サイドキャンバー（ SC）とは、スキーの最も狭い部分（ waist）でのスキーと、テールとショベルの最も広い点の間の直線距離のことです。 (Hirano and Tada, 1996; Kaps et al., 2001; Lind and Sanders, 2004; Federolf et al., 2010b) サイドカット半径（ＲＳＣ）とは、スキーを平面上で平らに押した状態(アーチベンドが０ )で、スキーの側面のショベル、ウエスト、テールの各点が交差する円の半径のことです。 (Kaps et al., 2001; Lind and Sanders, 2004)主な関数としてスキーの幅、厚さ、およびスキーを構成する材料の長さに沿って スキーの曲げ剛性は変化します。 (Howe, 2001; Lind and Sanders, 2004; Federolf et al., 2010b)スキーはさらに、各層間で接着されているので、スキーの製造中にプレストレスを受けています。その結果、荷重を受けていないスキーはキャンバーと呼ばれる曲がった形をしています。 (Howe, 2001; Lind and Sanders, 2004; Federolf et al., 2010b)撓み剛性の分布とともに、スキーのキャンバーは、スキーに荷重がかかったときにスキーの滑走面の下にかかる圧力の分布に影響を与えます。ねじれ剛性とは、スキーの長手方向軸の変形に抵抗するスキーの能力を指し（ Howe, 2001; Lind and Sanders, 2004）、曲げ剛性とともに、スキーをエッジングして荷重をかけたときにスキーの先端とテールが雪とどのように積極的に相互作用するかを決定する上で重要な役割を果たしています。 (LeMaster, 1999; Zorko et al., 2015 

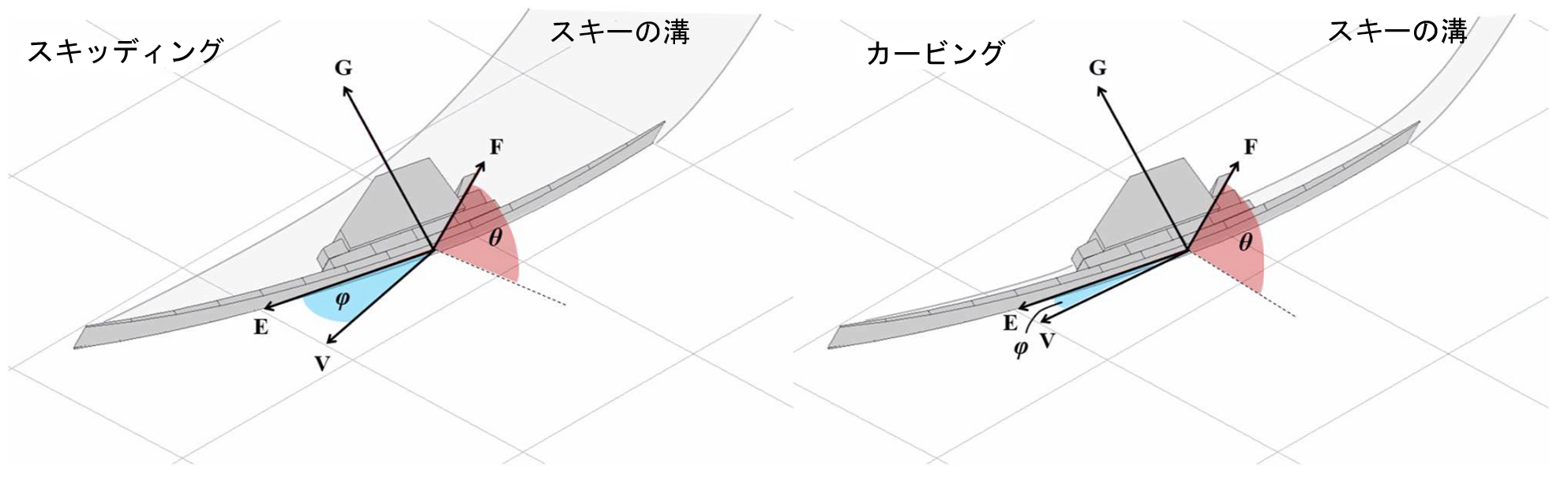
１－２： スキーリファレンスシステム 
スキーの機能を理解するためには、雪面に対するスキーの動きとオリエンテーションを定量化することが重要です。そのために、 Lieu (1982)と Lieu and Mote (1985)は、スキーの向きとその結果として得られる雪面との角度を定量化するための基準システムを導入しました。（図１）スキーの中心点を起点とする EFG 座標系は、スキーの位置と向きを定義します。E はスキーの長手方向軸に平行な方向であり、 F と G はそれぞれスキー底面に対して横方向と法線方向です。スキーと雪面との間にある 2つの角度は、スキーの機能を発揮する上で特に重要です。θは、局所的な雪面の平面とスキーの走行面との間の「エッジ角」であり、スキーが局所的な雪面に対してどの程度「エッジの上」で傾いているかを記述しています 。 スキーの「迎え角(attack angle)」（φ）は、スキーの長手方向軸Ｅと中心点の雪面に平行な平面内の速度ベクトルＶとの間の角度です。迎え角とは、スキーの長手方向の軸がスキーの進行方向に沿ってどの程度向いているかを説明するもので、スキーと雪の相互作用の性質に影響を与える重要な要素です。φはスキー全体の迎え角を表しているが、スキーの幾何学的性質、エッジングや荷重を受けて変形した形状、雪面に対する回転運動や並進運動などによって、スキーの長さに沿った各位置の局所的な迎え角は変化します。 (Hirano and Tada, 1996; LeMaster, 1999; Tada and Hirano, 2002; Hirano, 2006; Spörri et al., 2016b)一般的に、スキーの局所的な迎え角はスキーの後半部分よりもスキーの前半部分の方が大きく、これがスキーのターン動作に重要な役割を果たしています

１－３： スキッディングとカービング 

雪面に沿ったスキーの動きを説明するとき、一般的には 2つのプロセスが認識されています。カービング中、スキーの端に沿った 点は、スキーの進行方向に沿って、雪面の溝に対する横方向の変位が最小またはゼロになるようにして、スキーの弓形軌道に沿って移動します。(Lieu, 1982; Lieu and Mote, 1985; Brown and Outwater, 1989; Renshaw and Mote, 1989)これに対して、前に進むにつれて雪面を 横滑りして いるスキーは、スキッディングと言われています。 (LeMaster, 1999)スキッディングでは、 スキーのエッジ 上の 各点は、進んでいる各点の軌道に沿って進むのではなく 、雪面を横切るように新雪を切り裂いていきます。 (Lieu, 1982; Lieu and Mote, 1985; Brown and Outwater, 1989; Renshaw and Mote, 1989)ス キー専門家の用語では、スキー全体をスキーとカービングのどちらかで 表現することが多い です 。しかし、スキー 全長の それぞれの部分に沿ってカービングとスキッディングの両方が同時に起こる可能性があるため、このような分類は単純化しすぎ ではない でしょうか 。Lieu (Lieu, 1982)と Lieuと Mote (1985)は、一定半径、一定速度のターンを通るスキーの運動を数値的にモデル化し、 スキーの迎え角を小さくすることがスキー運動に与える影響を研究しました 。 彼らは、迎え角が約11度以上になると、スキーの長さに沿ったすべてのポイントがスキッドモードになることを発見しました。また、 迎え 角を 9度以下に下げると、スキーの後方からカービングが始まることを発見しました。迎え角のさらなる減少は、スキー板後半部がカービングに移行する範囲の増加と関連していました。しかし、高度なカービングの段階でも、 Lieuと Moteは、カー ビングがスキー板の後半部に限定されていることを発見しました。

１－４： カービングと溝の形成 

Lieu と Mote (1985) の発見は、「カービングスキーがどのようにしてスキー板の後半部が乗る溝を形成するのか」というメカニズムを説明するのに役立つ意味で重要です。 エッジを角付して荷重されたスキーの先端が雪面上の点を通過するとき、雪に接触するスキーの前の部分は、ねじりと たわみ では比較的柔らかく、荷重が重くないことが多いです。 したがって、スキーのこの部分は雪に貫入しない 代わりに雪面上を横にずれて 滑り たわみ とねじれ の両方で振動します。 スキーの 各点を通過するにつれ 、スキー前半の硬い部分が雪に当たり、最終的にはスキーを雪面に押し込むのに十分な圧力が発生します。この時点から、スキーはその後の通過点を通過するたびに雪の中に深く 貫入し続け、溝を発生させていきます。 (Tatsuno et al., 2009; Federolf et al., 2010b; Heinrich et al., 2010)圧力の上昇により貫入量が増して、雪が溝の側壁に徐々に圧縮されていきます。その両方が、ブーツが通過する際に発生する大きな力に備え て、溝の剪断に対する抵抗力を向上させます。(Mössner et al., 2006; Tatsuno et al., 2009)

図１

Lieuと Moteによって定義(1985)された、スキーエッジ角（θ）と迎え角（φ）θは、局所的な雪面の表面とスキーの走行面との間のエッジ角(角付け角)である。スキー板の迎え角（φ）は、スキー板の縦軸（ E）と中心の雪面に平行な平面に投影された中心点の速度ベクトル（ V）の間の角度です。左の図は、比較的大きな迎え角を持つ滑走例で、雪面に広い溝を掻き分けている様子を示しています。対照的に、右の図は雪の中に狭い溝を残して、迎え角の小さいカービング滑走例を提示しています。最大圧力のポイントから、スキーの残りの部分は、貫通(貫入)で比較的負荷がかからず、スキー前半部の通過によって生成された溝の中に乗ります。 このように見て 、 スキー板前半部は 厳密に言えば 、「 決してカービングをしない 」 ということになります。なぜなら、 研究文献と 、スキー 専門書の両方で予測されているように、スキー板前半部はエッジに沿った点が各々の軌跡をたどり、 その過程で新しい雪を削るからです

１－５： スキーの軌道 

カ ービングスキーの軌道をモデル化しようとする初期の試みは，スキーの幾何学的特性と，雪面にエッジをつけて荷重をかけたときの変形スキーの形状のみに基づいていた． Howe (2001) は、剛体で平面的な雪面に対して、変形したスキーの曲率半径 (RT ) をエッジ角 (θ ) とサイドカット半径 (RSC) に関連付ける式 (1) を提案しました。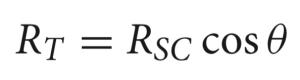

式(１ )：スキーの雪面への変形の度合いを大きくすることで、ＲＴが減少し、スキーのターン軌道がタイトになることが期待される。式（１）が示すように、その一つの方法として、 エッジ 角(角付け角)を大きくすることが挙げられる。スキーがエッジ上でターンをすると、雪面に接触するためにより多くたわむ必要があり、その結果、変形が大きくなり、有効な回転半径が小さくなります。この現象は多くの研究で実証されています。 (e.g., Heinririch et al., 2006; Federolf et al.,2010a; Mossner et al., 2010)同様に、スキーのサイドカットを大きくすると、スキーの曲げ変形が増幅され、結果としてRTが低下することがわかっています。 (Hirano and Tada,1996)このような経験的証拠があるに もかかわらず、式(1)はいくつかの重要な点で単純化しすぎています。第一に、雪面が非常に硬い時もありますが、実際には完全に硬くなることはありません。前述したように、スキーは雪面に貫入し、その深さは、荷重力、雪の貫入に対する抵抗力、およびエッジ 角に依存します。 (Lieu and Mote, 1985; Brown and Outwater, 1989; Tada and Hirano, 2002; Federolf, 2005) これはスキ ーの変形を増加させるので、 RTを式(1)で推定された値よりも低い値に減少させる必要があります。 (Howe, 2001; Kaps et al., 2001)このことから、 Howeは、 Cは接触長、 SCはサイドキャンバー、 DPは貫入の深さである非剛体雪面を考慮した式(2)を提案しました。 
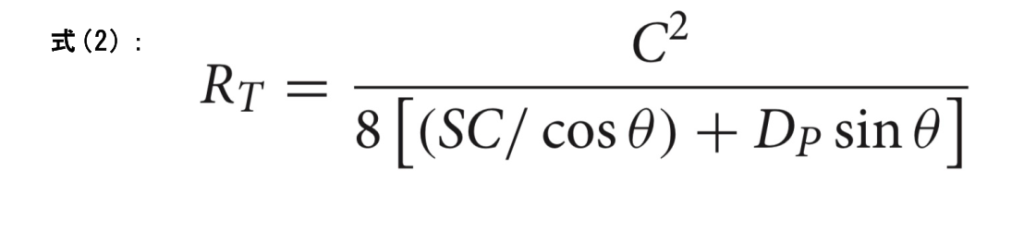式１と式２の 両方においての 第２の限界は、スキーエッジの全長が雪と接触してカービングしているという前提に基づいていることである。しかし、実際には、スキーのある部分は、局所的な滑走面圧、局所的なエッジ角度、 局所的な雪の剪断強度のバランスに応じて、カービングモードとスキッドモードを交互に繰り返すことがよくあります。最近、いくつかの研究者が、カービングスキーは、式1と式2の両方が仮定しているように、雪面上の偏向したエッジの形状で定義された軌道に正確に追従しないことを示す実験的証拠を報告しています。
ジャイアントスラロームのエリート選手を対象とした研究では、 Wimmer (2001)は、再構成されたスキー軌道から得られたスキーターン半径と、式1を用いて計算されたスキーターン半径との間には、わずかな相関関係（ r = 0.39-0.57）しかないことを発見しました。特に、実際のスキーターン半径が大きな値に近づき、計算されたターン半径が RSCの限界に近づくターン切り替え付近では、再構成されたターン半径と予測されたターン半径の間に大きな差があることが報告されています。

香川ら (2009)、辰野ら (2009)、米山ら (2008)は機械式のスキーを 用いてカービングターンでのスキーの変形を測定しました 。スキーの軌道は測定していませんが、実際のスキーのターン半径は、変形したスキーのエッジで定義された半径の約2倍と推定されました。こ れは、カービング中に溝が形成されるメカニズムと、スキーの前半部が雪をかき分けて溝を形成している間はカービングしないという考えに関連しています。
＜以下の記述は以前記事にしたチューリッヒ工科大学のドクター論文の評価です。私は全然理解できてなかったです＞
Federolf(2005)と Federolfら (2010b)は、ジャイアントスラロームターンでカービングスキーが雪中に残したコースを地中測量し、スキーの実際のターン半径を雪の浸透を考慮したHowe(2001)の式(式2)を用いた予測値と比較しました。 彼は、変形したスキーの予想される形状に基づいて予測されたターン半径が実際の対策を過小評価していることを発見し、スキーの前半部がカー ビングスキーの軌道で説明できる以上に大きく変形し、特にエッジ 角が高くなることを示しました。 Federolfら（ 2010a）は，溝形成の力学を取り入れたカ ービングスキーの有限要素シミュレーションを用いて，低いエッジ 角（ 40度未満）ではハ ウの方程式がシミュレーション結果とよく一致するが，高いエッジ 角では Howeの方程式がスキーのシミュレーションされたターン半径を過小評価していることを発見しました。カービングスキーの軌道が雪面上の変形した形状と必ずしも一致しないことは、スキーが雪面とどのように相互作用するかについて、研究者とスキー専門家の双方からの理解を深める上で課題となっています。この調査の目的は、スキーヤーの技術に関する以前の運動学的研究で測定されたスキー運動特性が、スキー雪の相互作用力学に関する我々の理論的理解に基づくスキー運動の予測にどの程度対応しているかを調べることでした。特に、我々の目的は、 (1)スキーの局所的な迎え角の測定値が、カービングがスキーの後半部に限定されているという Lieu and Mote (Lieu, 1982; Lieu and Mote, 1985)の予測にどの程度対応しているかを調べ、 (2)スキーの形状とエッジ 角に基づくターン半径に関する Howe (2001)の式(式1)が、実際のスキー軌道の測定値をどの程度予測しているかを調べることでした

●理解したこと
①スキー前部は、カービングターン中でもカービングでなくズレが発生していて振動状態、後部で
カービングして、最終的なカービングの軌跡跡が仕上がっている。
＝＞上級者における、上手い下手は、前部の扱いなのかと思う。上級者では、カービングターンの結果はほぼ同列で、差が見えないので、前部の振動部分でどう抑え込んでいるかで差がでそう。選手でいえば、速さが前部のコントロールなのかもしれない。前部と後部のバランスもスピードに関連するとおもう。
②角付け角とターン弧については、式１と式２があって、式１は、角付け角４０度未満で合っているが
４０度以上だと合わない

ＳＴＡ２４でも、角付け角とターン弧の接線方向角との関係が円状になることが判っています　

●以後
STA24のデータを使って公式１の検証をやってみます。
それを基に、STA25のシステム構成を決めていきます。
迎え角とカービング角を測定するために、センターにBaseアンテナを設置して
前に迎え角用のRoverアンテナ、後ろにカーブ角用のRoverアンテナが必要
判りましたので、１Base ２Roverでいくことにします。