IMUでGYRO積分角を測定したのはいいのですが、足に付けたIMUの姿勢が時時刻刻と変化する場合に
地面の基準座標に対して、どうやって変換していけばいいのかについて、基礎から学習始めました。
●回転行列の必要性
IMU BNO055からの姿勢角は、加速度センサの重力加速度成分とGyroの角速度、磁気センサの地磁気方位がありますが、今回は、地磁気センサ無し(精度が悪いのと応答が遅い20Hz)で、Gravityからpitch rollを算出して、Gyro角速度を積分して、回転変位角のを得ます。これらセンサ座標でのセンサの姿勢表現から、地表面の基準座標での回転角度変位を得るために、センサ座標から基準座標への変換が必要です。座標変換方法には、表現のやり方が何通りもあって、どれを選ぶかは、ユーザー次第です。クォータニオンだけで処理したい人もいますが、
私の場合は、回転を物理的に目視で理解したいので、回転行列RxRyRzの積からRzyx Rxyzを作って回転行列変換を行います。
この場合、回転させ方で、変換方法が違うのですが、センサの出力に合うように変換させるので、積の順番がどうであれ結果が
センサ出力と合致すればよいので、方法の選択は自由です。
●私の最大の課題 3次元座標回転で、回転方式と変換行列が直観的に理解できない
私は、直観重視の技術者なので、自分の目で見て、頭の中で動かせるモノしかイメージがわきません。3次元の座標回転は
行列式では、すぐ回転結果がでるのですが、その3次元座標を目視するにもExcelでは、良いグラフがありません。
とりあえず、3面図で座標の回転を追いながら、直観的理解を深めます。
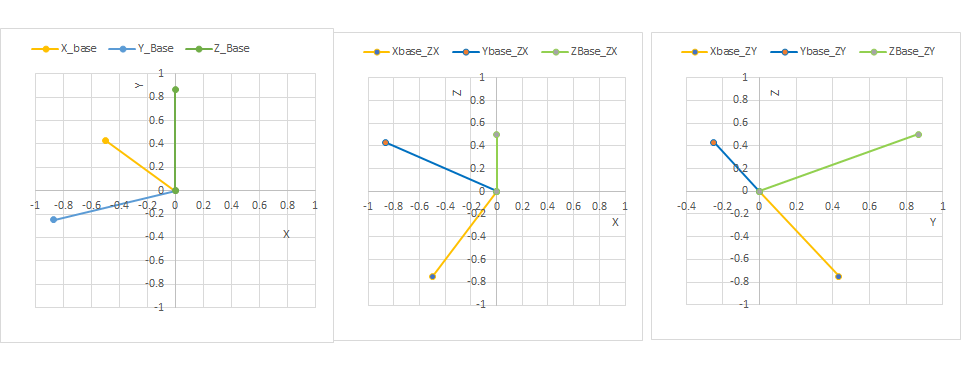
●2次元グラフを3面でXY面 XZ面 YZ面で表示してみた
Z軸を傾けることで、Z軸のXY面への投影像が見えます、Z軸を傾けるとXY軸がZ座標にのめりこむので、いずれの座標も長さは短くなります。これでも、とりあえず頭の中の数値と座標値の関係で理解してみます。
将来的には、スキー解析のグラフィクスとして、C#で3Dグラフィクスライブラリで作ってみます。
■3Dグラフィクスの基礎リンク
https://learn.microsoft.com/ja-jp/dotnet/desktop/wpf/graphics-multimedia/3-d-graphics-overview?view=netframeworkdesktop-4.8
http://kanamori.cs.tsukuba.ac.jp/lecture/old2017/cg_basics/03/03_slides.pdf
とりあえず「EXCEL VBAで回転行列作って、座標をプロットして目視で、3次元回転を実感したい」
ということで、2日かけて、EXCEL VBAで座標を回転させる簡単なマクロ作りました。
ポイント1:見え方がどうなるか試行錯誤なので、入力が自在で、即グラフで見られる機能が必要
ポイント2:回転方式がオイラー式と固定角式があるので、両方に対応したものにする
ポイント3:次のバージョンで、センサデータとグラフを対応させるための機能も用意しておく
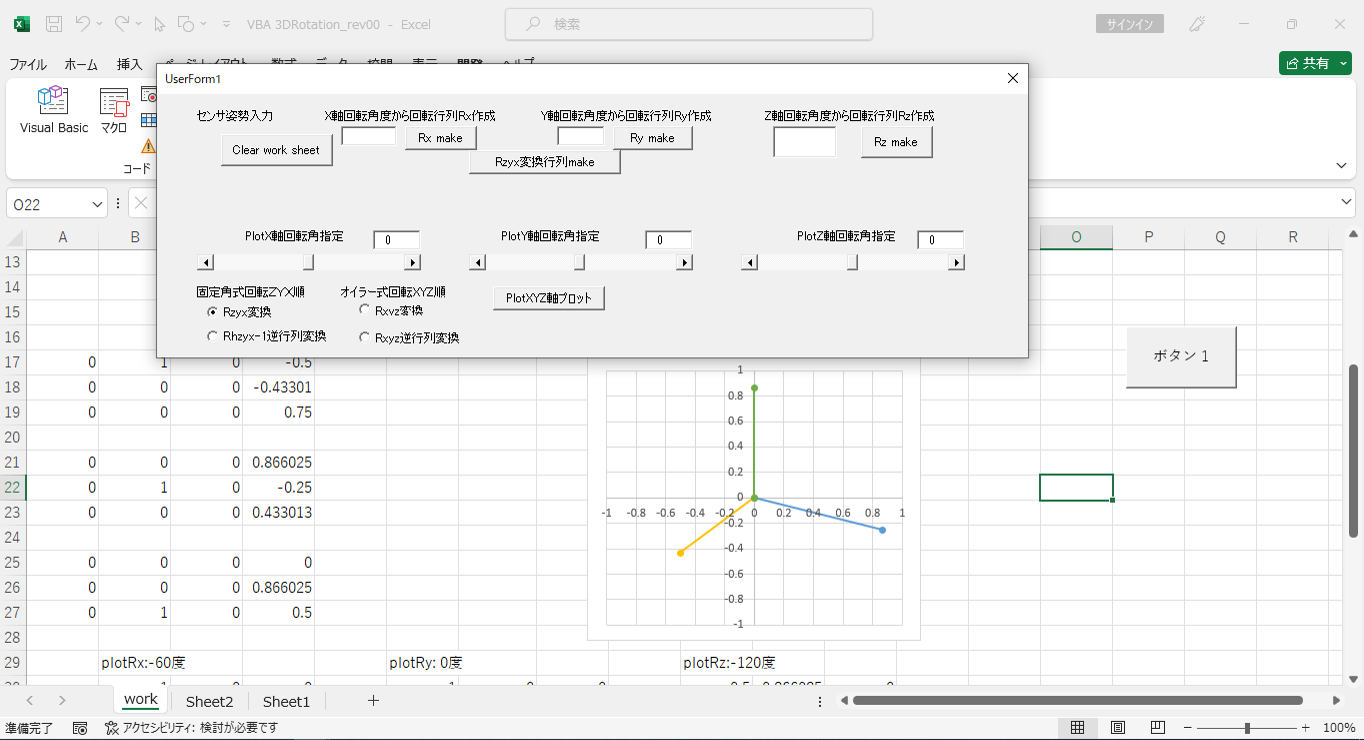
●EXCEL 3次元座標回転ツール
原理は、XY座標で3次元表現するために、座標軸を回転させて見えないZ軸も投影で見えるようにして、3軸のXY面への投影をみています。XY平面とXZ平面とYZ平面の3面を表示します。Excel2021でVBAで作ってあります。
注意)ダウンロードして走らせるときに、外部のマクロのセキュリティ警告がでて起動できなくなりますので、MSのページの解説をみてセキュリティ設定を変更してみてください。
更に、任意の変換されたベクトルもプロットできるようにします。
※マクロファイルですのでワンタッチでダウンロードできません、ブラウザのダウンロード履歴をみて、安全でないファイルと言われてダウンロード拒否されてますので、強制的にダウンロードするにしてダウンロードしてください。このファイル危険はないです。
VBA 3DRotation_rev01
ZIPは、
VBA3DRotation_rev01
※2024年11月12日 マクロファイルがダウンロードができなくなっていたようで、すみませんでした。修復しました。
概要:VBAフォームに各軸の回転角度を入力すると、シートの散布図のXYZ座標が回転します
角度と座標の見え方を体験する単純なマクロです。
機能1:スライドバーでX軸、Y軸、Z軸の回転角度を指定できます。TextBoxに直接書き込みでも指定できます。
PlotXYZ軸プロット ボタンを押すと、シートのグラフにその回転角度で3次元回転プロットがでます。
機能2:回転行列の積の順序の違いで、どのように、回転が変わるか体感できます。(固定角式とオイラー式で回転が違います)
固定角式だと回転した座標を見ながら所望の姿勢にもっていくのが大変難しいです。回転するのが基準座標なため。
オイラー式だと、回転した座標その軸を何度回せばいいか、直観的にわかりやすいです。回転毎の軸を回わす方式のため
使い方:デフォルトでは、OptionButtonは、固定角のRzyx変換になってます。
ダウンロードして、シート workのボタン1を押すとフォームがでてくるので、
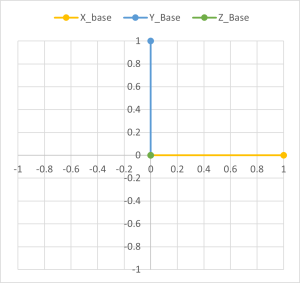
初期値は全部0度なので、PlotXYZ軸プロット ボタンを押すと、シートの小さいグラフが
下記のように、X軸(黄土色)とY軸(青)がでます。z軸(緑)は、ゼロ点から上に向かってます
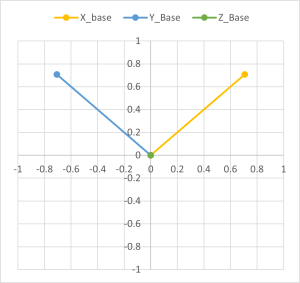
次にZ軸を45度回転させてみます。フォームのPlotZ軸角度指定でスクロールバーもしくはTextBoxに
45といれて、PlotXYZ軸プロット ボタンを押すと右図のように+45度回転します。
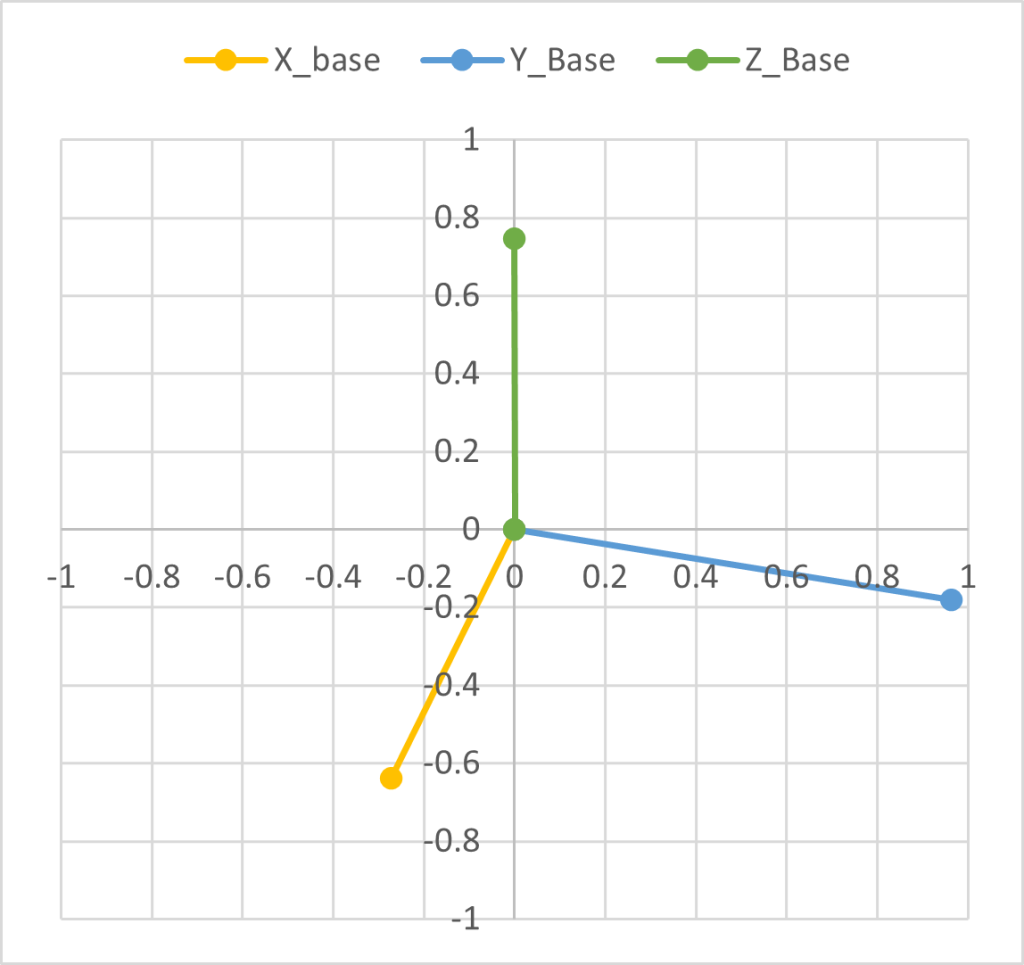
これだけだと3次元風にならないので、X軸17度 Y軸 -46度 Z軸 ー113度といれてプロットすると
3次元風に座標軸が見えてきます。この図を作るのに、10分くらい試行錯誤しました。固定角式だとなかなか
回転のイメージがわきませんので、5度くらいずつ左右に動かしながら数値とグラフの動きを対比させならがやりました。
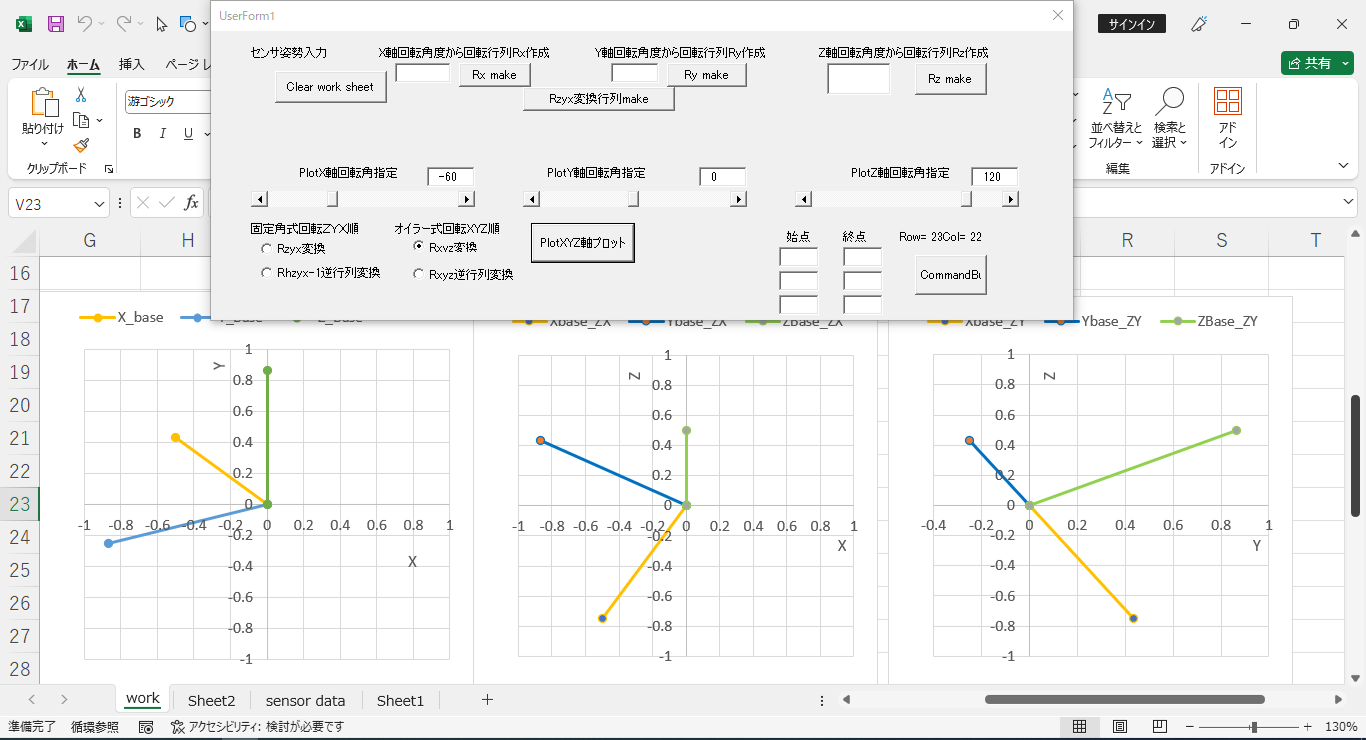
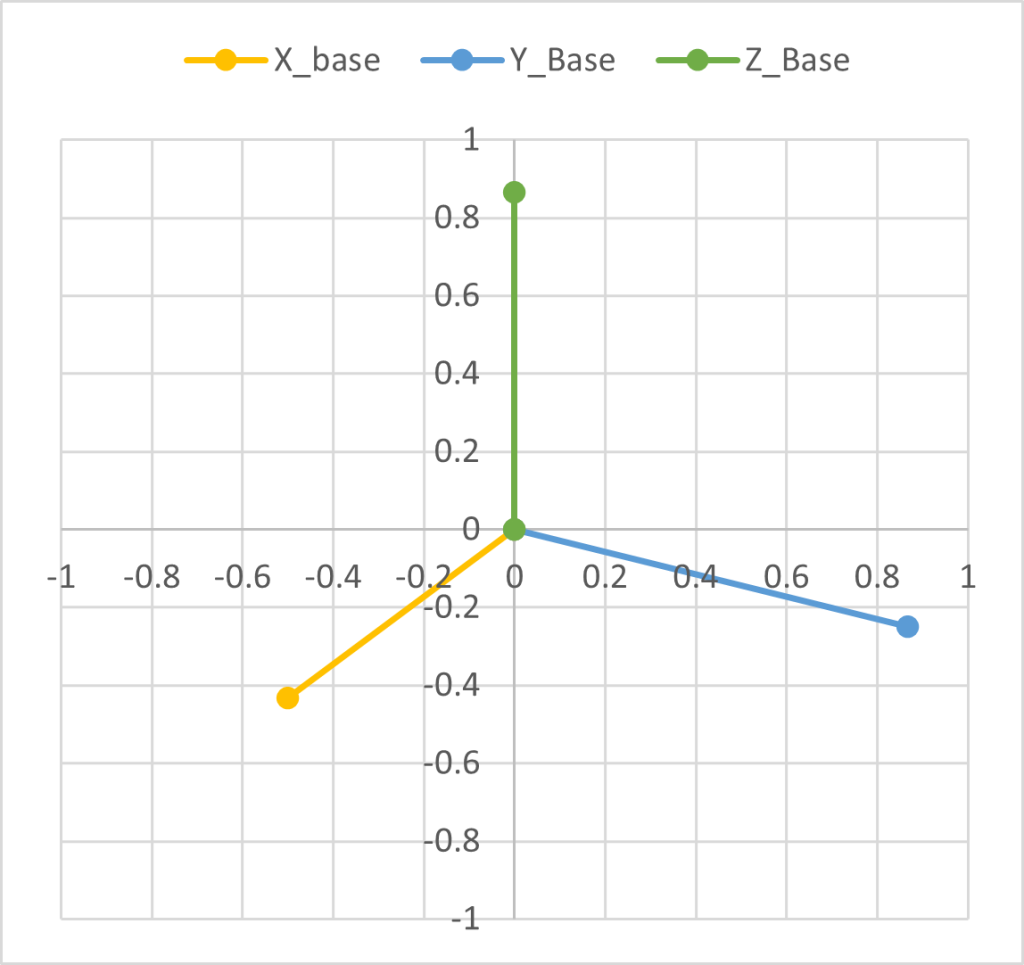
●オイラー式のほうがやりやすい
下図にもっていくのに4回だけの試行でできます。今見えている軸を何度くらい回せばいいか直観的にわかるからです。
角度は、固定式と全然ちがいます。-60度、0度、120度でした。
●VBA 行列計算TIPS
VBAの配列では、行列関数が使えないので、いちいち配列をセルに代入する手間があります。
あらかじめシート上に行列の位置をきめておいて、Rangeで場所ごと定義しておけば、配列の代入が1行ですみます。
以下は、各行列をRangeで定義して、積算した結果をRangeに代入してます。
Set rng1 = Range(Cells(2, 1), Cells(4, 3)) ‘Rx range
Set rng2 = Range(Cells(2, 5), Cells(4, 7)) ‘Ry range
Set rng3 = Range(Cells(2, 9), Cells(4, 11)) ‘Rz range
Set rng4 = Range(Cells(8, 1), Cells(10, 3)) ‘Rzy range
Set rng5 = Range(Cells(8, 5), Cells(10, 7)) ‘Rzyx 変換行列完成range
Set rng6 = Range(Cells(13, 5), Cells(15, 7)) ‘Rzyx逆行列 range
Set rng7 = Range(Cells(13, 9), Cells(15, 11)) ‘Rzyx転置行列 range
Set rng8 = Range(Cells(13, 13), Cells(15, 15)) ‘Rzyx逆行列 x Rx 検算
Dim arr As Variant
arr = WorksheetFunction.MMult(rng3, rng2) ‘Z * Y 積
Worksheets(“work”).Cells(7, 1).Value = “zyx回転行列積 RzxRy部”
Range(Cells(8, 1), Cells(10, 3)).Value = arr
Worksheets(“work”).Cells(7, 5).Value = “zyx回転行列積 Rzyz完成(センサ=>基準座標変換)”
arr = WorksheetFunction.MMult(rng4, rng1) ‘Rzy * X 積
rng5.Value = arr ‘変換行列完成
‘逆行列と転置と検算
Worksheets(“work”).Cells(12, 5).Value = “zyx回転行列逆行列(基準座標=>センサ座標変換)”
arr = WorksheetFunction.MInverse(rng5) ‘Rzy * X 積
rng6.Value = arr ‘逆行列
‘転置
Worksheets(“work”).Cells(12, 5).Value = “zyx回転行列逆行列(基準座標=>センサ座標変換)”
arr = WorksheetFunction.Transpose(rng5) ‘Rzy * X 積
rng7.Value = arr ‘転置行列
‘検算 Rzyx-1*Rzxy
Worksheets(“work”).Cells(12, 5).Value = “zyx回転行列逆行列(基準座標=>センサ座標変換)”
arr = WorksheetFunction.MMult(rng6, rng5) ‘Rzy-1 * Rzyx 積
rng8.Value = arr ‘逆行列
●学習の参考になっているリンクに感謝
WEB上では、回転行列とオイラー角の解説記事は膨大にありますが、なかなか自分に合ったものがありません
今回は、こちらの記事を見ながら、学習させていただきました。tech blog様に感謝
https://daily-tech.hatenablog.com/entry/2017/11/19/025248
オイラー角,固定角,回転行列...
この記事の丁寧な図解を見て、VBAマクロを作ろうとおもいました。良い図に感謝です。
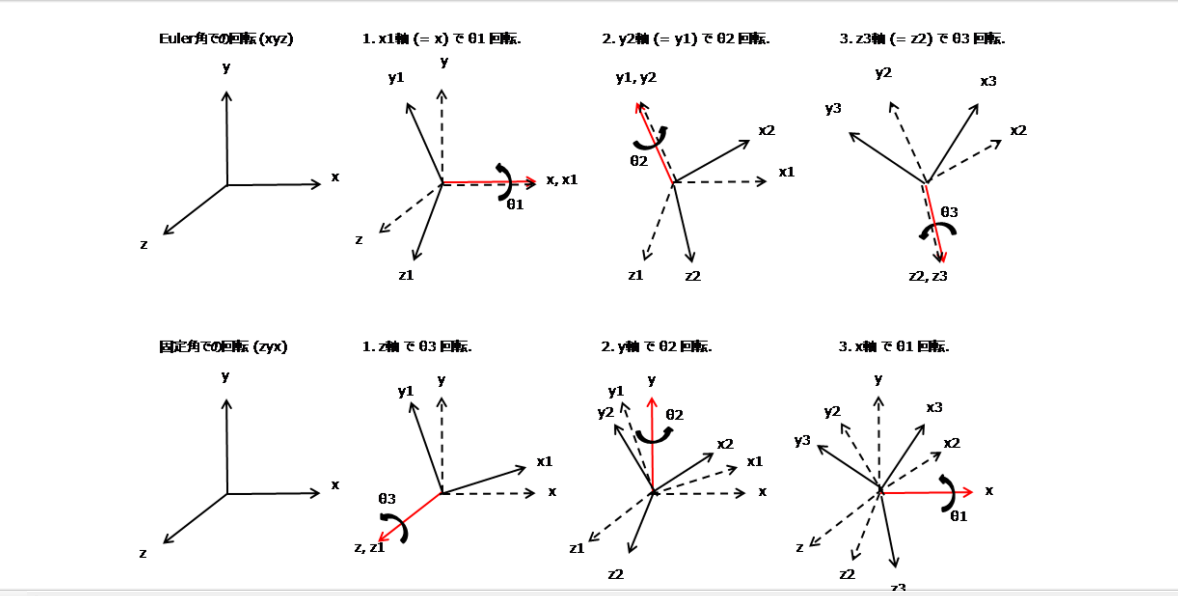
他にもたくさんあるので、リンク列挙させていただきます。
オイラー角の順序組み合わせは数十通りもあるそうで、用途によって、順序がきまっているそうです、
①回転行列の基本
https://www.sky-engin.jp/blog/rotation-matrix/
②3次元ベクトル基本
https://watako-lab.com/2019/01/23/roll_pitch_yaw/
③座標変換の基本
https://rikei-tawamure.com/entry/2019/11/04/184049
④オイラー角の種類
https://www.sky-engin.jp/blog/eulerian-angles/
https://qiita.com/take4eng/items/0f5a9ff47fd345e5fc33
●以後
いじりながら、イメージをわくようにして、センサ角度対応のマクロを作っていきます。