干渉補正をEXCEL手動計算から、Processingのプログラムでの計算に引っ越し中です。
Processingの行列ライブラリーの使い方練習と一般逆行列計算練習をしてみました。
●Processingの行列計算ライブラリー Pallav.Matrix

ProcessingIDEに標準でインストールできるようになってます。しかし、内容がわからないので、GITから全ファイルダウンロードします。
Pallav.Matrixというライブラリーです。
https://github.com/pallav12/matrix-library-for-processing
referenceフォルダーに一覧があります。
ダウンロードして、解凍するとMatrixMathというフォルダーができます。MatrixMath->examples->sampleUseCases.pdeがあるので、
processingで起動して走らせます。
ライブラリーの関数のサンプル動作を並べてあります。
特徴1:行列の表記のために Matrix.print()関数があります。
float [][] a={ {1,2,3},{4,5,6},{7,8,9} };と定義すると
Matrix.print(a);
{ { 1,2,3},{4,5,6},{7,8,9} }
のようにコンソールに出力してくれます。
特徴2:行列の表現は2次元配列ですが、普通の配列数と
Matrix型の両方を使えるようになってます。
両者を使い分け方がわかりません。同様に使えます。
配列からMatrix型に変換する関数
Matrix mat_a=Matrix.array(a); では配列aが行列式mat_aになります
特徴3:転置関数は、正方行列でしか動作しません。
しかし、一般逆行列は、矩形行列が基本ですので、Pallav.Matrixの
転置関数 Matrix.traspose()は使えません。
そこで、自分で矩形行列用の転置関数を作りました。
簡単な計算なので、無事一発で走りました。
array_Srcに転置する元の配列、array_Transに転置結果の配列
| ///======Rectangular Matrix Transpose==================================== void Rect_trans(float [][] array_Src,float [][] array_Trans) { int Rnum,Cnum; int i,j,k; Rnum=array_Src.length; Cnum=array_Src[0].length; println(“Rnum=”,Rnum,”Cnum=”,Cnum); for(j=0;j<Cnum;j++) { for (i=0;i<Rnum;i++) { //println(“array_src[“,i,”][“,j,”]=”,array_Src[i][j]); array_Trans[j][i]=array_Src[i][j]; } } //Matrix.print(“array_Src=”,array_Src); //Matrix.print(“array_Trans=”,array_Trans); } |
●Processingプログラムで動作確認と一般逆行列計算学習
サンプルで使う行列データは、こちらの記事からいただいて、グラフもそっくりそのままいただきました。
「大人になってからの再学習」様に感謝です。http://zellij.hatenablog.com/entry/20120811/p1
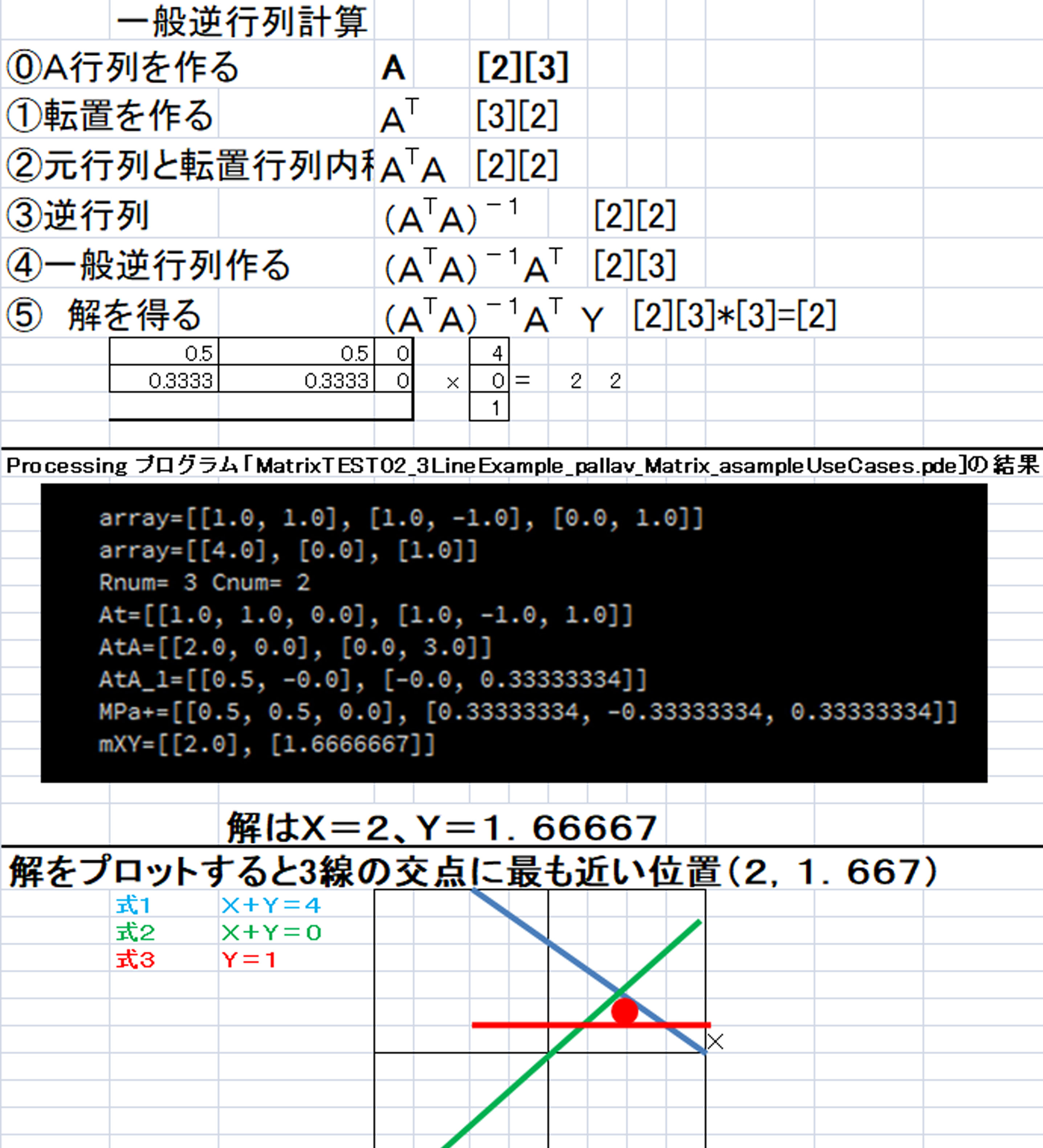
①全体の考え方
わざと解がない連立方程式を作って、近似解を一般逆行列で解かせる学習サンプルです。

これの解をだしたProcessingプログラムは、GISTに掲載してあります。
https://gist.github.com/dj1711572002/e27b093453b8f4eefd4e0d58d7c56359
MatrixTEST02_3LineExample_pallav_Matrix_asampleUseCases.pde
| import pallav.Matrix.*; //Processing Matrix Libraly //Demonstrating use of some of the static Methods of library // MatrixTEST00_pallav_Matrix_asampleUseCases.pde // ==========Shinshu-Makers MatrixLibrary Study no1============================= int m = 3, n = 2; float[][] A={{1,1},{1,-1},{0,1}}; //A data array float[][]B={ {4},{0},{1} }; //B const array float[][] At=new float [n][m]; float[][] AtA=new float[n][n];// Square Matrix float[][] AtA_1=new float[n][n];//Inverse Matrix float[][] MPA=new float[m][m];// Moore_Penrose Inverse Matrix float [][] XY=new float[1][2];// Calcuration Resultvoid setup() { Matrix.print(“array=”,A); Matrix.print(“array=”,B); Rect_trans(A,At);//Traspose Rectangular Matrix X Matrix.print(“At=”,At); AtA=Matrix.Multiply(At,A);// Multiply Xt X then SquareMatrix get Matrix.print(“AtA=”,AtA); AtA_1=Matrix.inverse(AtA);//Inverse Matrix Matrix.print(“AtA_1=”,AtA_1); Matrix mAt=Matrix.array(At);//Matrix henkan Matrix mAtA=Matrix.array(AtA);//Matrix henkan Matrix mAtA_1=Matrix.array(AtA_1);//Matrix henkan Matrix mMPA=Matrix.Multiply(mAtA_1,mAt);// Moore-Penrose Inverse Matrix XtX*Xt Matrix.print(“MPa+=”,mMPA); Matrix mB=Matrix.array(B); //Matrix mXY=Matrix.array(XY); Matrix mXY=Matrix.Multiply(mMPA,mB); Matrix.print(“mXY=”,mXY); } ///======Rectangular Matrix Transpose==================================== void Rect_trans(float [][] array_Src,float [][] array_Trans) { int Rnum,Cnum; int i,j,k; Rnum=array_Src.length; Cnum=array_Src[0].length; println(“Rnum=”,Rnum,”Cnum=”,Cnum); for(j=0;j<Cnum;j++) { for (i=0;i<Rnum;i++) { //println(“array_src[“,i,”][“,j,”]=”,array_Src[i][j]); array_Trans[j][i]=array_Src[i][j];}} //Matrix.print(“array_Src=”,array_Src); //Matrix.print(“array_Trans=”,array_Trans); } //============================================================== |
●以後
やってみれば簡単なので、慣れればいいだけでした。
これを基本にして、リアルタイムで、干渉補正するシステムを作り出します。
7月いっぱいでできればいいなと考えてます。