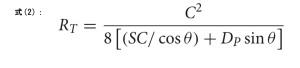Norwayの学者さんの論文を読みながら、STA24で測定したデータと照合する作業をしてます。
PythonでターンRの円近似をしたり、ターン回りのパラメータをあれこれ作って相関をみました。
●結果
①論文の式に合っているか
式１ Rtがターン弧、RscがスキーのサイドカーブR Θが角付角
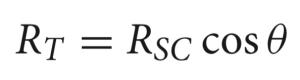
式２ C エッジの雪面接触長、SC サイドカーブ Dp 雪面入り込み深さ Θ 角付け角
CとDpが見当がつかないので、この式は確認できませんでした。
式１は、非常に単純な式ですが、私の測定データでは、全くあてはまりませんでした。
原因：私のターンは、角付角が２０度前後と小さく、ズラして曲がっている
各パラメータの相関関係をみました・
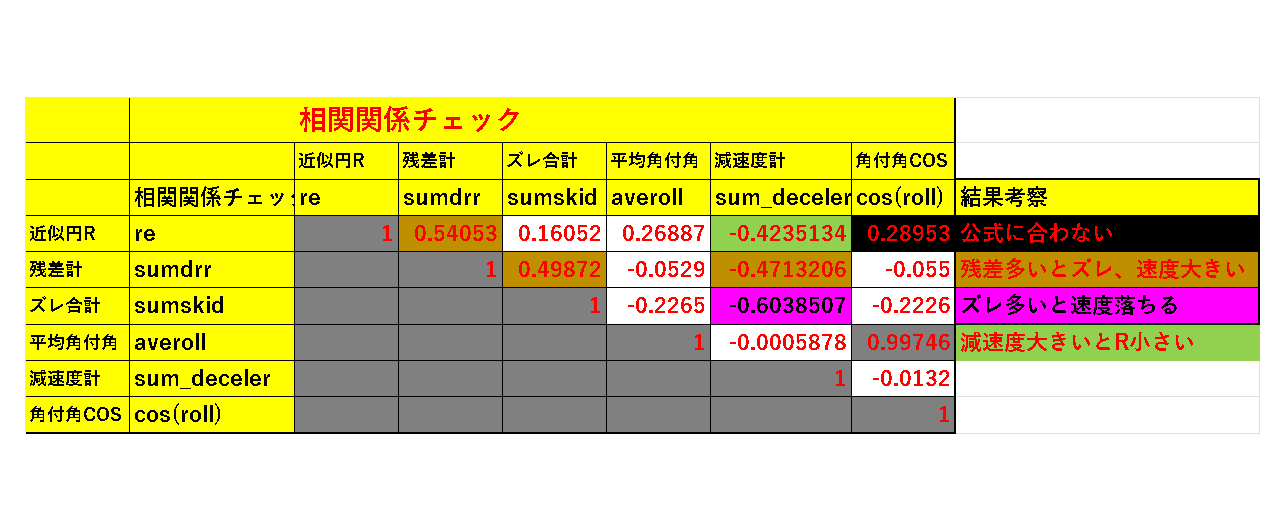最も相関高いのが、ズレ角の合計と減速度の合計、ズレが多いと速度遅くなると当然の結果です、
円のRと相関が高いのは、残差（近似円と実際のターン弧の誤差）Rが大きいほど、誤差が大きくなる
減速度大きいとターン弧は小さくなる
テーブル
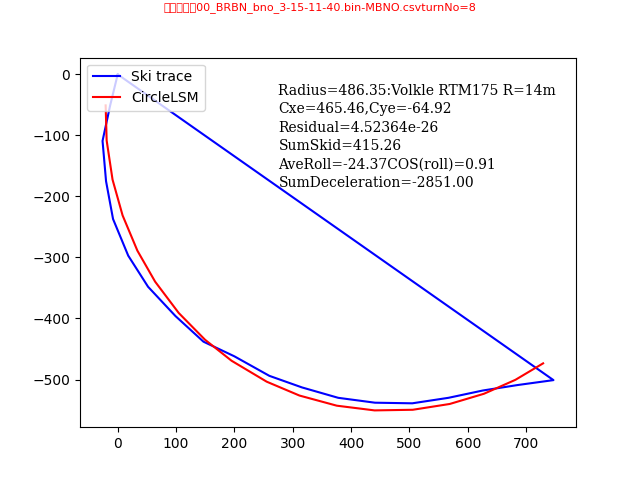
②ターン弧のグラフ
最もズレ角が少なかったターン１８＝＞近似円とよく重なっている、
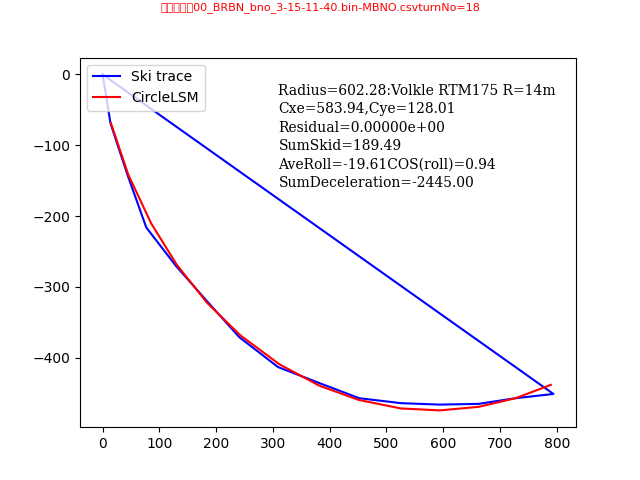ダメなターン 残渣が大きく、ズレも大きい、円弧とターン軌跡が大きくずれてる
●やり方
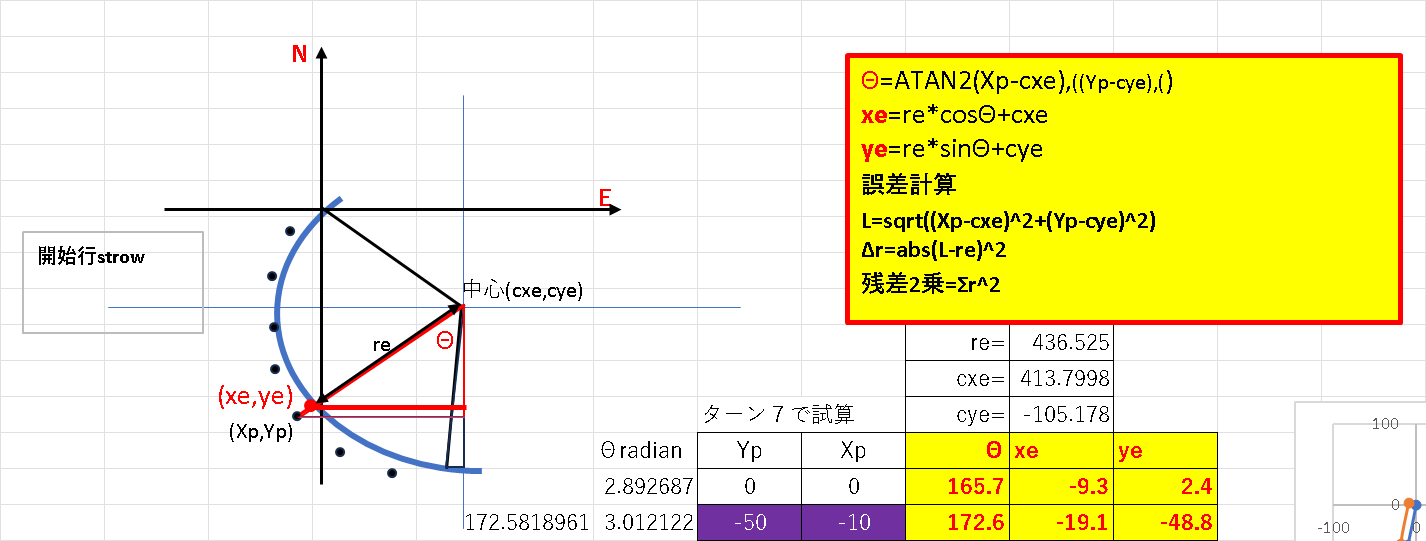
python プログラムで、ターン毎に円近似して、グラフプロットしてパラメータを記入した
GIST https://gist.github.com/dj1711572002/8078304b0da08d58665549870cd395fc
円の最小二乗法は、WEB上にたくさんあります。
残差は、自分で作成しました。実データと近似円の半径の差を二乗した計を残差としてます
●論文の内容との考察
①今回の結果で、近似円に近いターンほどズレが少なく残差もすくないので、良いターンとなる。
公式に納涼なターンが上手なターンと考えてよいと思う、STA25でプロライダーのデータで検証する。
②論文のメインは、スキー前部で迎え角とターンの挙動ですが、次回の記事で学習します。
