補間したデータをいろいろな処理で、精度を改善する補正方法を模索してます。
まずは、データ間の相関を一括して眺められる seaborn pairplotをしてみました。
●seaborn pairplot
これは、有名なプロットですが、dfから1発でコラム間の相関プロットが全組み合わせみられる優れものライブラリーです。
matplot の補強ライブラリーで matplotがインストールされてないと動きません。
●基本的なプロット
①seabornをインストール
コマンドプロンプトで以下入力ENTERで自動ダウンロードしてインストールしてくれます。
| pip install seaborn |
②プログラムでimport行追加
|
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from scipy import interpolate
import pandas as pd
|
③DataFrame を作成して、pairplotをプロット
gは、後で使うために作っておく
|
g=sns.pairplot(df)
|
③グラフを画面に表示させる
上記だけでは、プログラム内ではグラフは生成されますが画面には出てきませんので
| plt.show() |
④結果
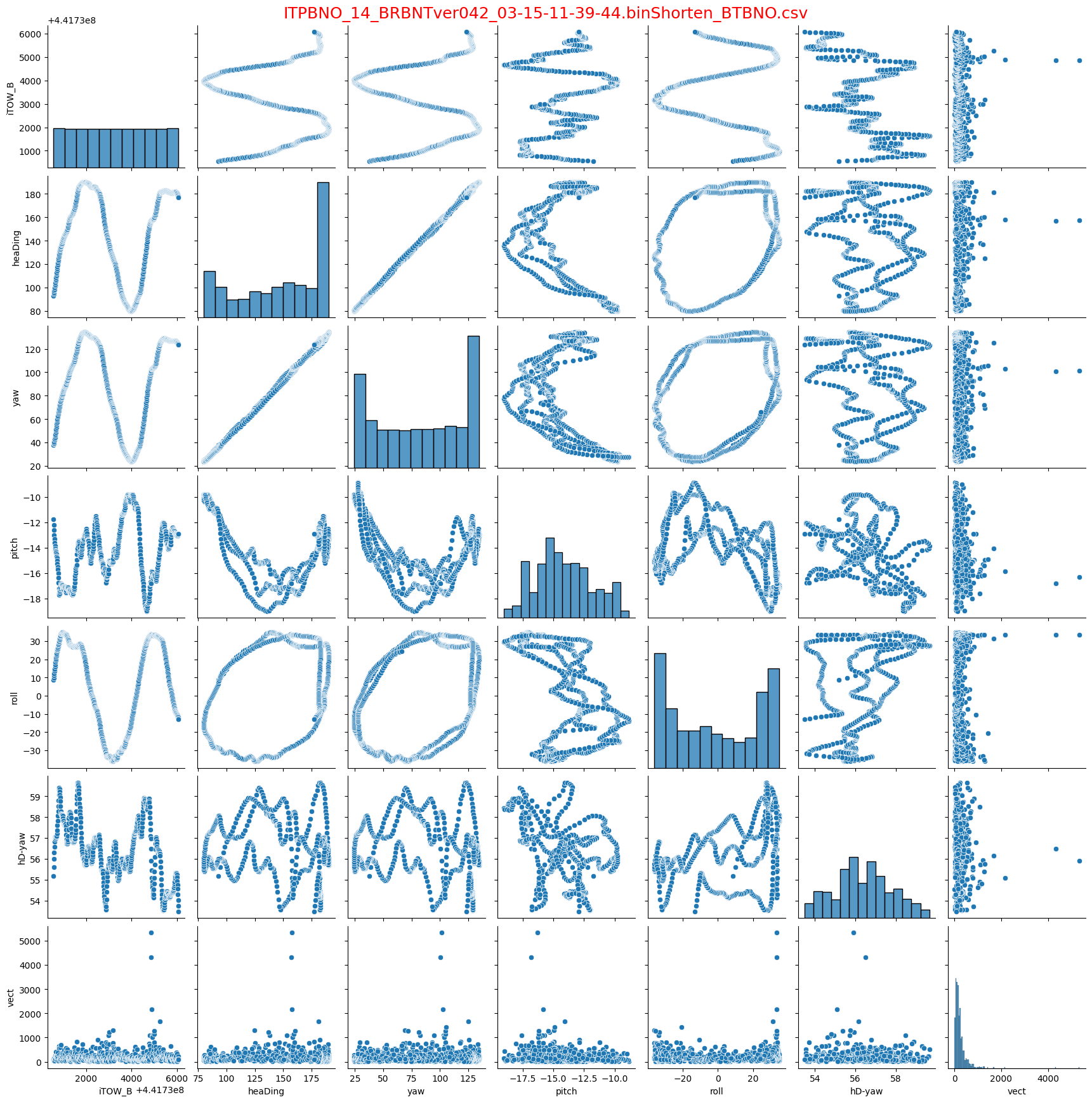
たくさんグラフが並んでますが、相関関係をプロットしてます。対角線で上下対称になります。対角線上のグラフは、ヒストグラム(そのパラメータの分布)になります。
グラフのdfのカラム順でここでは、iTOW_B,heaDing,yaw,pitch,roll,hD-yaw(Heading角-yaw各),vect(加速度ベクトル大きさ2乗ax^2+ay^2+az^2)
見たいポイント:hD-yaw値がyaw角のHeading角との差ですので、この値が一定値になれば、誤差が少ないことになりますので、hD-yaw値を中心に眺めます。
⑤pairplotのタイトルの付け方
普通のグラフではないので、タイトルの付け方備忘録しておきます。
g=sns.pirplot(df)とplt.show()の間の位置にいれます。
※ここで文字位置の数値y=0.995とありますが、1以上だと上からはみ出してしまって見えませんが、0.9だと下すぎてグラフの中にタイトル文字がはいってしまうので、
0.995ときわどい数値”TITLE”でなく、str形式の文字変数も使えます。
|
g.fig.suptitle(”TITLE”, y=0.995,size=18, weight=2, color=”red”)
|
●実際のプログラム
以上の基本動作を確認してから、実際に使うプログラムを作成しました。
データが大きいので、スキーターン1-2ターンずつ切り取ってあるcsvを作っておいて、読み込んでdfにして、paireplotさせて、グラフ画像を保存するプログラムです。
キーボードからのキーインでいろいろな動作するので、今回のpairplotは’a’キーを押すと動作するので、elif v==’a’以下の行で記述してあります。
全体はこちら https://gist.github.com/dj1711572002/17cb86c73d494291ca7de628c16dc4a7
元のCSVでは、11カラムあるので、11x11のpairplotを描くと時間がかかるので、必要なパラメータを絞って新たなdf_pplotを作成してpairplotしてます。
|
elif v==’a’ :#RTK補
print(“Anlysys”)
print(“>>>> SELECT ITPBNO FILE”)
root = tkinter.Tk()
root.withdraw()
iDir = r’C:/RTK_Log/hokan’
fTyp = [(“BNOデータファイル”, “*.csv;*.xlsx;*.xls”), (“すべてのファイル”, “*.*”)]
filename = FileDialog.askopenfilename(parent=root, initialdir=iDir, filetypes=fTyp)
# filenameからbasenameをとりだしてファイル種類区別
basenameITP = os.path.basename(filename) #読み込むCSVファイルの名前だけ抽出
df_ITPBNO = pd.read_csv(filename, low_memory=True) #CSV読み込み
print(“df_ITPBNO:”,df_ITPBNO.shape,basenameITP)
df_ITPBNO[“vect”]=df_ITPBNO[“ax”]**2+df_ITPBNO[“ay”]**2+df_ITPBNO[“az”]**2 #加速度を2乗して和をvectとして列作成
print(df_ITPBNO)
df_pplot=df_ITPBNO[[“iTOW_B”,”heaDing”,”yaw”,”pitch”,”roll”,”hD-yaw”,”vect”]] # 必要なパラメータだけ抽出して新たなdf_pplotを作成
g=sns.pairplot(df_pplot) #pairplot実行
g.fig.suptitle(basenameITP, y=0.995,size=18, weight=2, color=”red”) # y= some height>1 #タイトルをつける
g.savefig(‘C:/RTK_Log/hokan/ITPparirplot’+basenameITP+’.png’) # グラフと保存
plt.show() #画面にグラフ表示
|
●解析
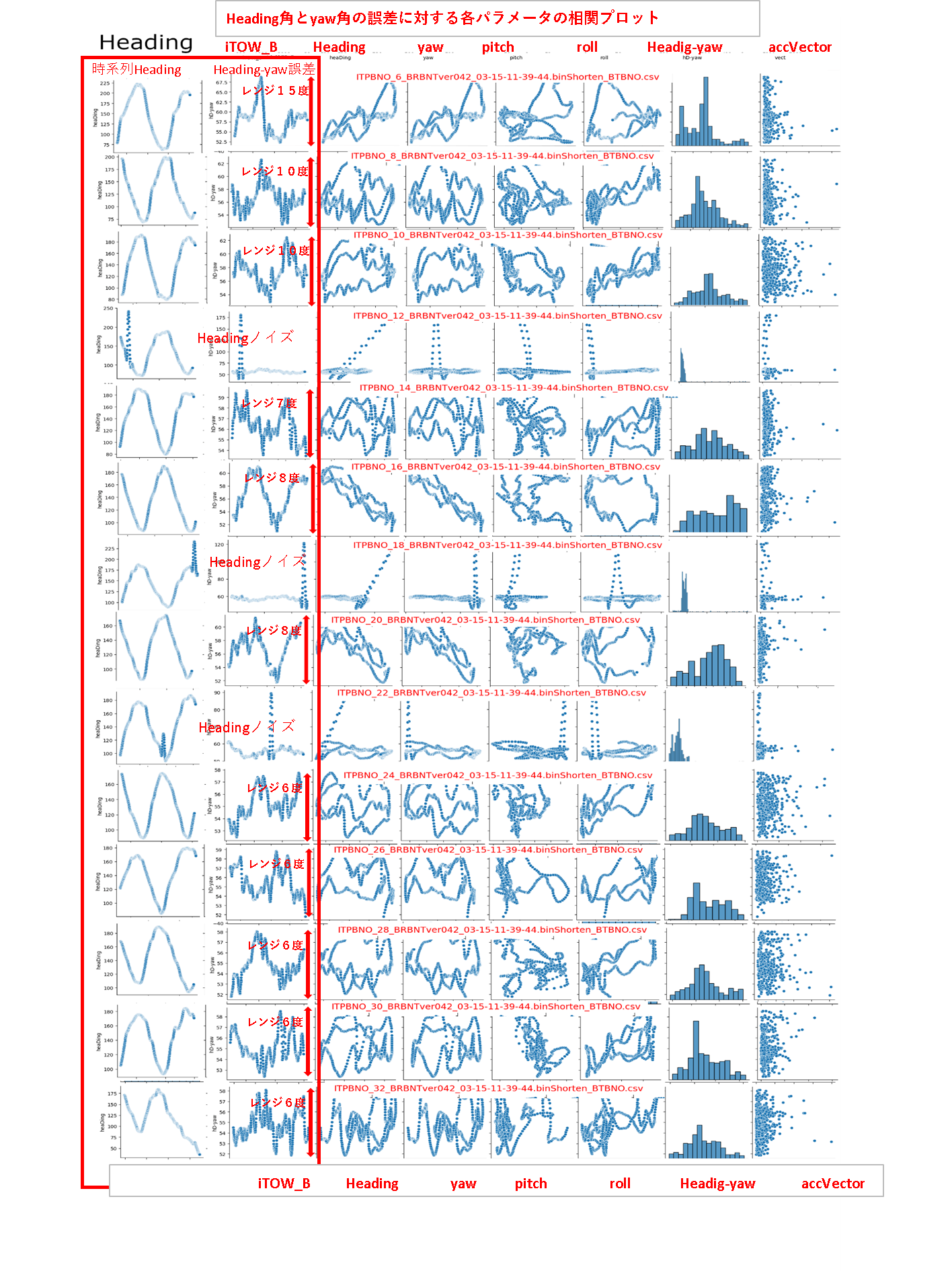
その1:誤差のそれぞれのパラメータの相関だけグラフを切り取って並べてみた。
※Heading角にノイズがはいっているデータは、大きくなってしまって使えませんでした。後でノイズ部分を除去して使います。
※左列のグラフが時系(iTOW_B)列のHeading角です。
結果:誤差のレンジは、最初の4段までは10度以上誤差がありますが、下半分の5段は、7度以下ですので、±3.5度以内に収まってます。
相関を眺めていても、誤差レンジ10度以上と誤差レンジ7度以下の区別がつきません。
その2:誤差であるhD-yawの値をhue=”hD-yaw”としてプロットすると全体で階調表現で影響が見えます。
|
# g=sns.pairplot(df_pplot)
g=sns.pairplot(df_pplot,hue=”hD-yaw”) # hue表示に変更
|
①hueの見方
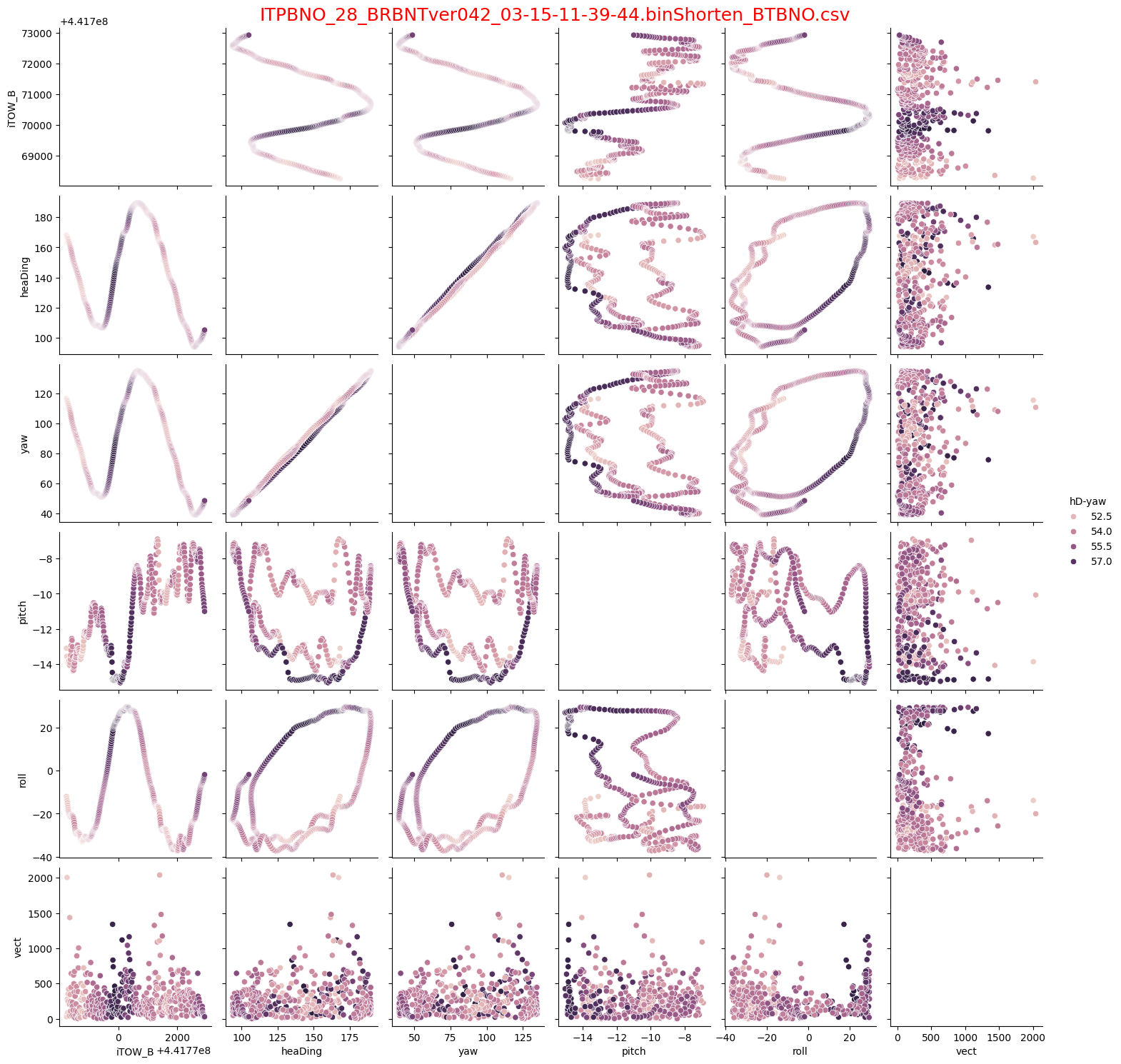
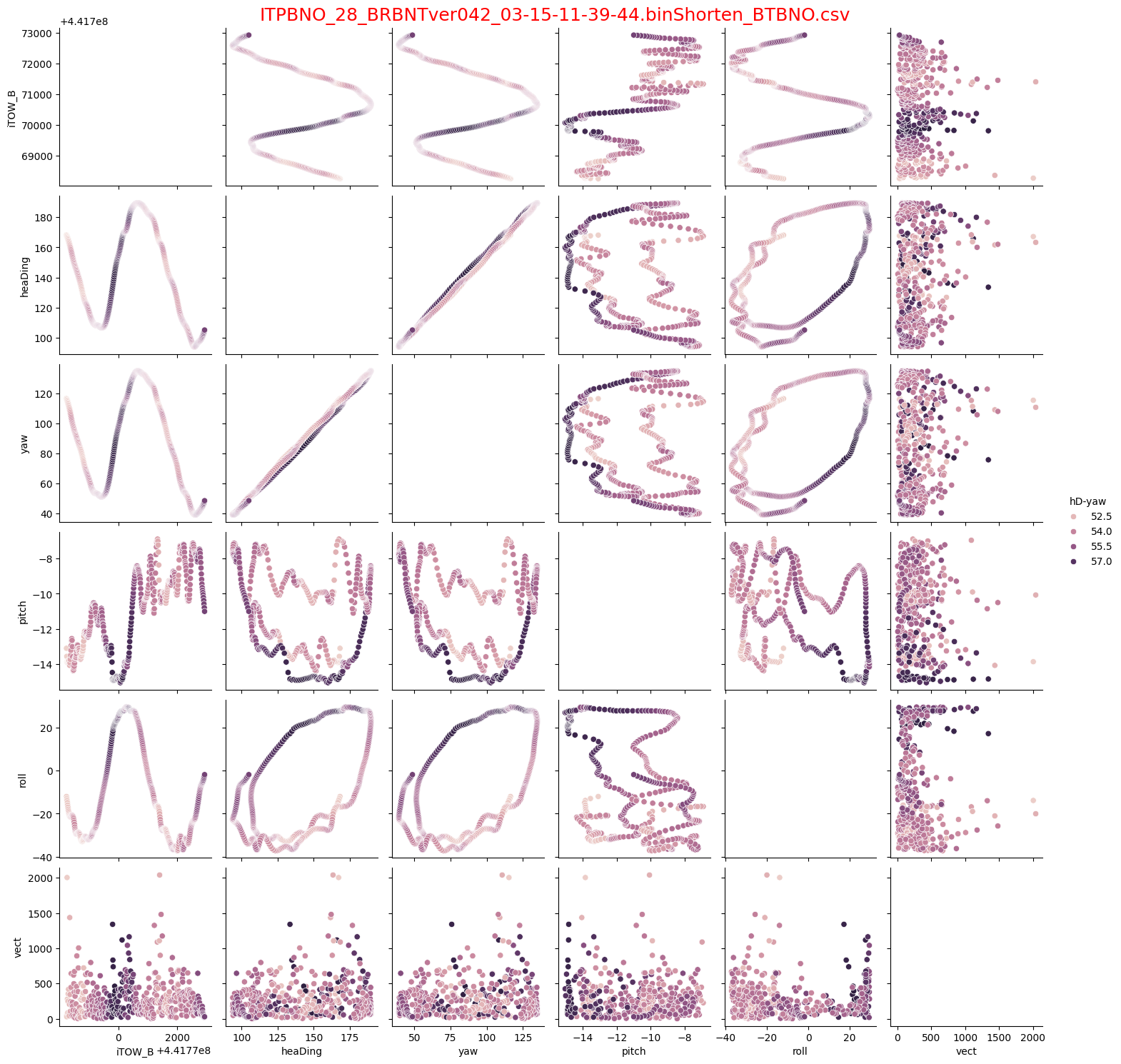
このグラフは28番データで、誤差レンジ7度です。右端にHUEの凡例がついているので、それをまず注目すると57度~52.5度の4水準で階調表現で、hD-yaw値を表現しておくことで全グラフにおけるhD-yawの値をプロットできてますので、相関へのhD-yawの影響が良く見えるようになりました。
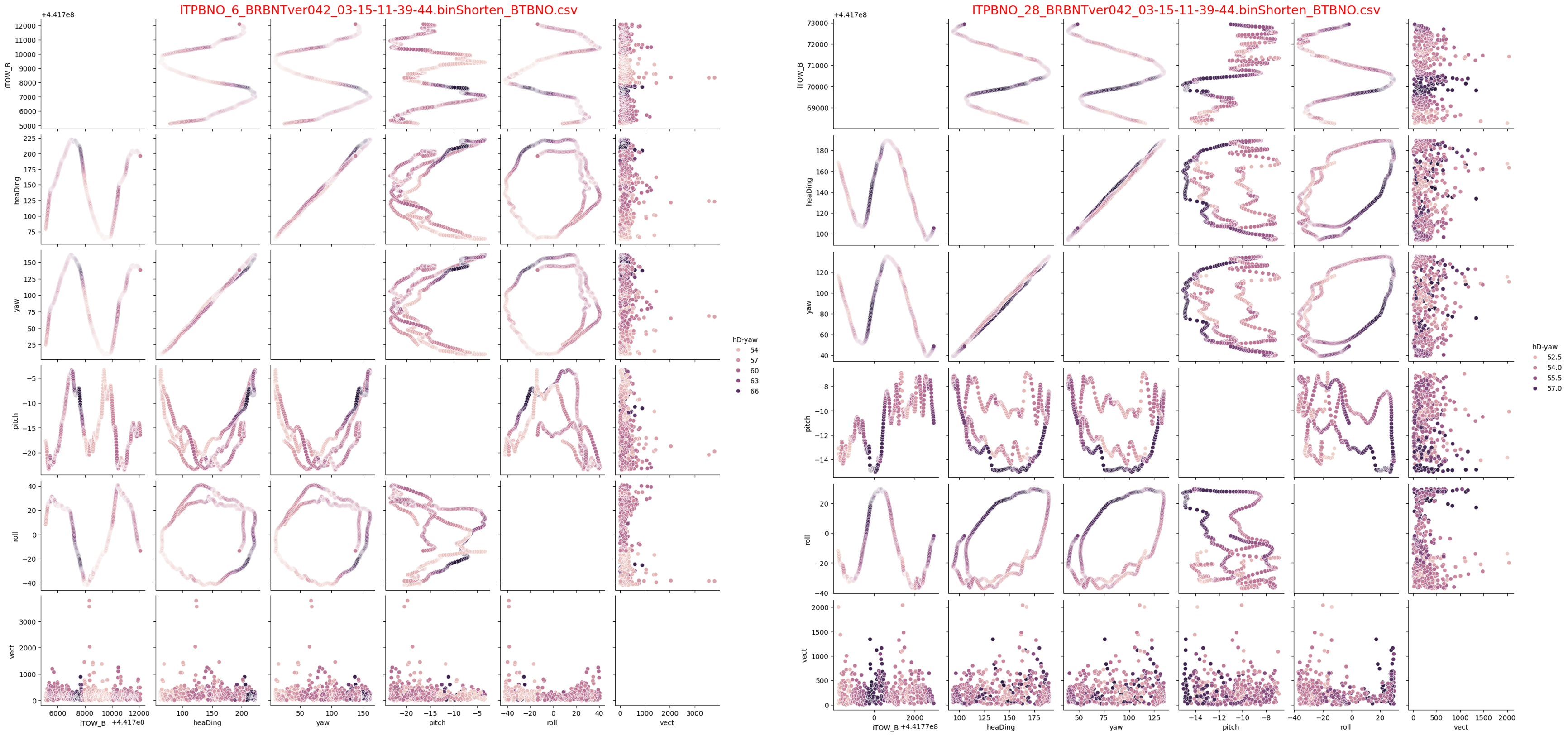
②上のHUEグラフと誤差レンジが大きいHUEグラフを並べ違いを観察することにしました。
左が6番データで誤差レンジ15度最悪のデータです。右が28番データで誤差レンジ7度の良いデータです。
左のHUE範囲は、54度~66度の階調です。
右のHUE範囲は、57度~52.5度です。
色の濃いところに注目すると
左のグラフは。時系列のピークから少し下がった範囲が濃くなってます。
右のグラフは、時系列のピーク以外の曲線が濃くなっています。濃い部分が多いのは、同じ色が多い=ばらつきが少ないということです。
=>ばらつきの多いグラフでピークを過ぎた範囲で、pitch rollも端っこ位置が濃くなってます。
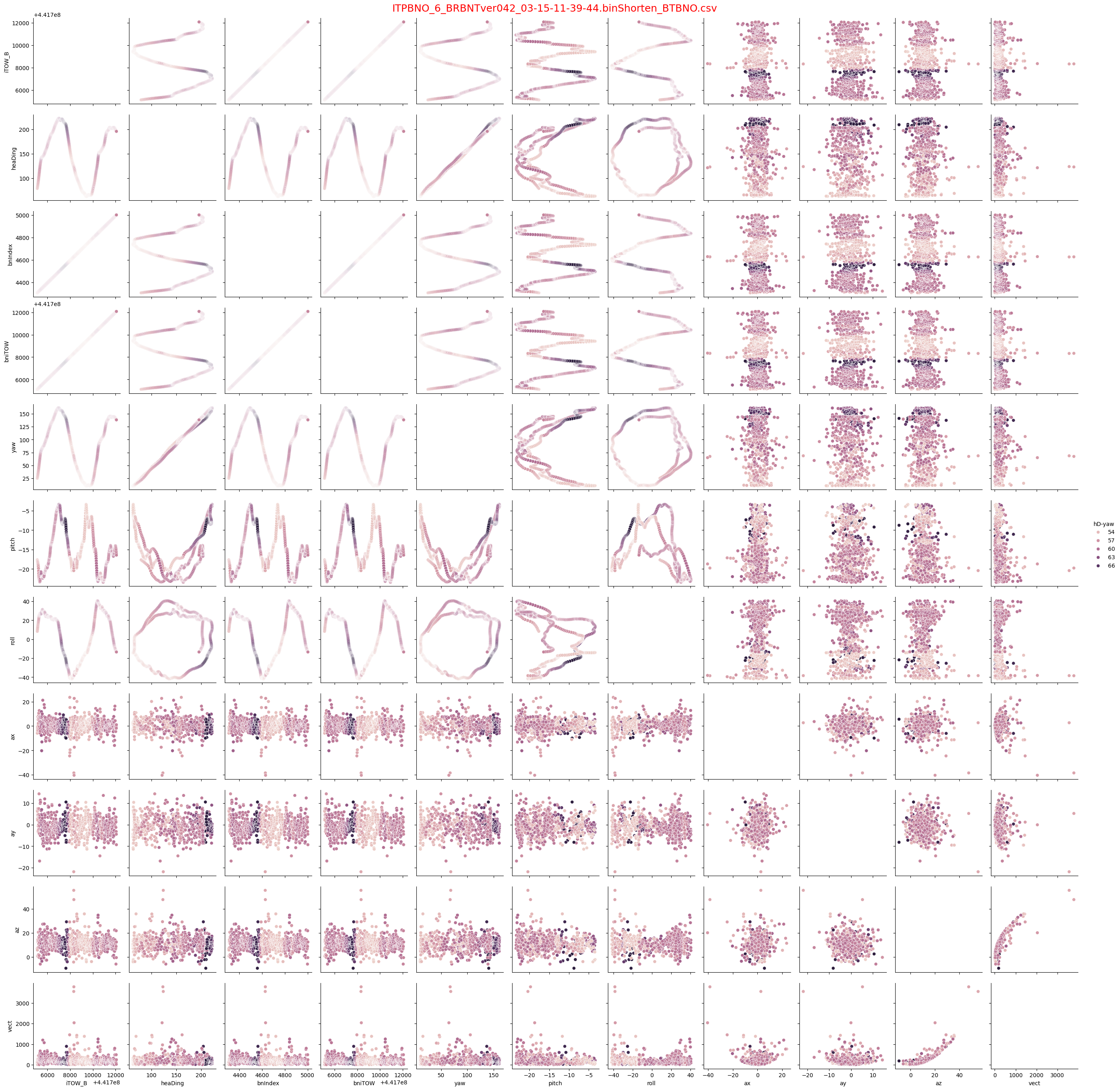
③パラメータの見落としがあるといけないので、全パラメータのHUEグラフもプロットしました。
誤差レンジが15度と大きい6番データでax,ay,azも加えたHUEグラフです。
濃い部分が特定箇所で発生しているのが顕著ですので、なんらかの関係性があるかもしれません。
●次は機械学習させてみる
誤差範囲の8度以上を区分する機械学習をトライしてみます。
昨年加速j度センサで基礎実験したときを思い出しながらやってみす。昨年の記事