スキー競技の論文を検索していて、今までは物理、力学論文が多かったのですが、今回の論文は、実践的です。
ノルウェイ、スイス、オーストリアとスキー大国の研究者達が共同で研究した論文です。
2020年、2021年ワールドカップ4大会のスーパー大回転の前走者にシステムを装着させて計測した、本物のコースと一流選手を使ってます。
滑降、スーパー大回転での選手の怪我の確率が40%程度あるという課題に対して、旗門とコース設定での安全性を図る取り組みの一環として
研究された論文です。人の命が係わる研究なので、測量用GNSS機器を使用して実測されてました。
残念なことに、RTKでなくdGNSSを使って測定していたので、精度が悪い計測になってしまってます。RTKができない環境だったのかもしれません。
信州MAIKERSのSTAとの違いは、スキー板の挙動を計測してない点です。目的が全然違うので、比較する意味ないですが、
選手のヘルメットにアンテナをつけただけの測位しかしてません。おおがかりなのは、コースを精密に測量している点が凄いです。
★論文2021年1月:
Injury prevention in Super-G alpine ski racing through course design
この論文を日本で紹介されていたサイト クラブアルペン情報局 様に感謝です。
スーパーGにおけるコースデザインによる怪我の予防
●内容概略
| 抜粋 | 私の理解 | |
| 本研究でやること | 最近の研究では、地形の傾斜、ターンの進入速度、コース設定が技術系種目のスキーヤーのスピードに影響を与えることがわかっている。GSでは、ゲートのオフセットを大きくしても、ゲートの垂直距離を短くしても、どちらも速度が低下することがわかっている。しかし、ゲートオフセットを大きくしてスピードを下げると、インパルス(選手の身体的努力の指標となる外力の時間的統合、レース中の疲労につながる努力)の増加、最小回転半径の減少、最大力の増加などにより、怪我のリスクが高まりましたが、ゲートの垂直距離を短くしても、このような怪我のリスクの高まりはありませんでした。しかし、Super-GにおいてもGSで実証されたような方法でスピードをコントロールできるかどうかは不明であり、Super-Gにおいても同様の定量的な推奨事項が作成できれば有益である。また,コース設定の操作が,旋回半径,インパルス,地面反力などの他の傷害リスク要因に及ぼす負の副作用を明らかにすることも有益である。そこで、本研究では以下を目的とした。(1) コース設定の特徴,入口速度,地形の傾斜がターン時の速度に影響を与えるかどうかを評価する. | 安全のためスピードを落とさせるために、 ①旗門の振れ幅を大きくしてスピードを落とせるが弊害がある。 1:選手に負担がかかる 2;回転半径が小さくなる 3:加速度が大きくなる などでメリットがない ②旗門の進行方向間隔を短縮するとスピードは落ちる コース設定によって、傷害のリスク要因を定量的に明らかにすることは、意義がある。そのため コースの設定の特徴 入口速度 地形の傾斜の影響 を評価する |
| 使用 機材 |
①GPS受信機 dBNSS 50Hzで測定、RTK100Hz測位も使えるが、本計測はdGNSS dGNSS: Alpha-G3T receivers with GrAnt-G3T antenna (Javad, USA) https://www.javad.com/product/alpha-series/  |
|
| GNSSアンテナ G5ant1 Antcom製 https://hexagondownloads.blob.core.windows.net/public/Antcom/Pdfs/Product-Sheets/PS-G5Ant-1XXX-S.pdf  |
航空機用軽量2波長GNSSアンテナ を選手のヘルメット前部にとりつけた。 |
|
| コース地形測量システム LEICA TPS1230 http://www.ys2000.net/leica/tps.html  |
1平米につき3ポイント測定した、 | |
| 測定
方法 |
データ収集 スタート地点、折り返し地点、ゴール地点、および地形は、それぞれのレースの前に、静的dGNSS:Alpha-G3T受信機とGrAnt-G3Tアンテナ(Javad社、米国)およびLeica TPS 1230 +(Leica Geosystems AG社、スイス)を用いて捕捉しました。雪面を十分に詳細に再現するために、平均して1m2あたり0.3点を測定しました。地形の移行部ではこの数が大幅に増加し、均一な地形では減少しました。スキー中のアスリートのトラッキングは,アスリートが背中とヘルメットに装着したハイエンドのディファレンシャル・グローバル・ナビゲーション・サテライト・システム(dGNSS)を用いて行われました。GPS/GLONASSの2周波(L1/L2)受信機(Alpha-G3T, Javad, USA)は,50Hzでアンテナ位置を収集した。アンテナ(G5Ant-2AT1, Antcom, USA)は前走者の頭部に装着した。搬送波位相二重差位置解を計算するために,2つの(冗長性のための)基地局をコースのスタート地点に設置し,GNSSアンテナ(GrAnt-G3T,Javad,USA)とAlpha-G3T受信機(Javad,USA)を装備した。 |
RTKより精度が劣るdGNSSで何故測定したのか理由は書いてないが、数cmが必要な研究ではないためだと思われる。
|
| データ 処理 |
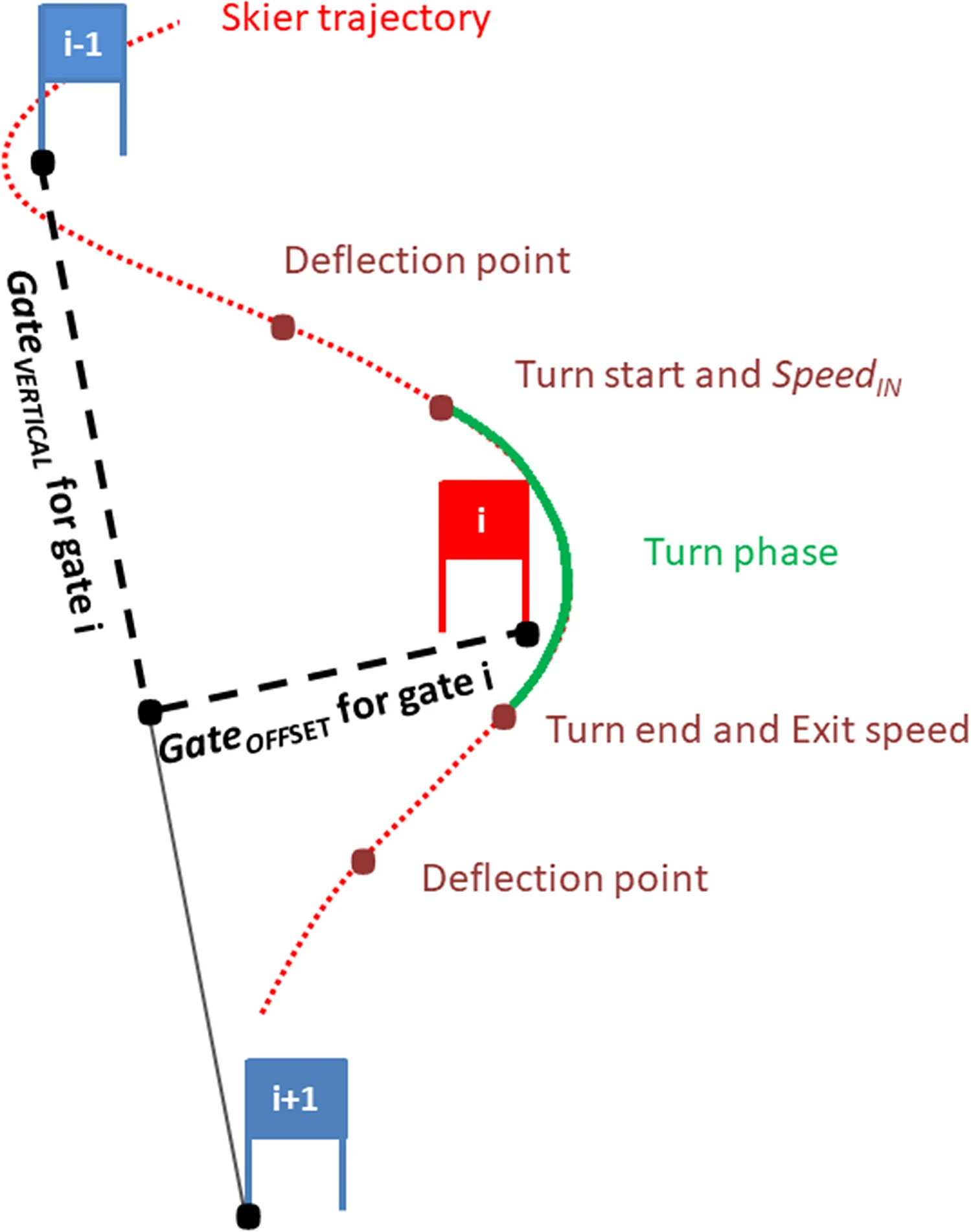
スキーヤーの軌跡と雪面の測地復元 雪面を表現するための地形表面上の静的なdGNSS測定、およびコースを表現するためのゲート位置は、測地学的GNSSソフトウェアJustin(Javad, San Jose, USA)を使用して、後処理手順で計算されました。スキーヤーのアンテナ位置データを算出するために,GPSおよびGLONASS衛星と周波数L1/L2から,測地学ソフトウェア(GrafNav NovAtel Inc., Canada)のKARアルゴリズムを用いて,二重差搬送波位相解を処理した。測地線のアンビギュイティが解消されなかったターンは調査対象から除外した。コース特性の算出 静止したdGNSSを用いて雪面の形状を測量しました。dGNSSで取得した点群をDelaunay法で三角測量してデジタル地形モデルを作成し、長方形のグリッドでグリッド化しました。地形の局所的な傾斜は,局所的な地形面の法線ベクトルを用いて幾何学的に導出した。曲がり角の平均的な傾斜を表現するために,曲がり角に関連する局所的な傾斜ベクトルを各曲がり角の面積で平均化した.この平均的なターンの傾斜をTerrainINCLINEと名付け、水平に対する角度で表した。アルペンスキーのコースには、ゲートが設置されており、スキーヤーが通るラインの外側には、ターン用のゲートとゲートが設置されている。コースの設定は、2つのゲートの距離によって特徴づけられる。すなわち、垂直方向のゲートの距離(GateVERTICAL)とゲートのオフセット(GateOFFSET)である。旋回するゲート間のユークリッド距離(線形ゲート距離とも呼ばれる)は、線形ゲート距離がGateVERTICALに線形的に大きく依存し、GateOFFSETには依存しないため、分析には加えなかった。GateVERTICALは、Gilgienらに示されているように、ゲート(i – 1)から(i – 1)と(i + 1)の間のベクトルへのゲート(i)の投影までの距離である。ゲート(i)のGateOFFSETは、ゲート(I – 1)からゲート(i + 1)までのベクトルへのゲート(i)の正規投影として計算した。連続する2つのゲートがディレイターン(2つのゲートでマークされた長いターン)を形成する場合、より大きなGateOFFSETを持つゲートがターンを表すものとして選択された。 |
汎用の測量アプリを使っているところをみると 研究者は、DIYでシステムを作るスキルがないみたいです。 やはり、これからの研究者は、DIYで処理プログラムを作成できるようにならないと独創的な研究成果がでないと思います。TerrainINCREMENT 地形の局所的な傾斜 曲がり角毎の傾斜角を曲がり角面積で平均化して水平に対する角度としたGateVERTICAL 2旗門間の標高差 GateOFFSET ゲート間の直線から離れた垂線距離 |
| 図 | コース設定特性の定義を黒で表示:垂直方向のゲート距離(GateVERTICAL)とゲートオフセット(GateOFFSET)。旋回フェーズは緑で着色されている。赤色:旋回フェーズは2つの偏向点内で、重心旋回半径が75m以下になったところから始まり、重心旋回半径が75mを超えたところで終わる。 旋回開始時の速度(SpeedIN)と旋回終了時の速度を計測する。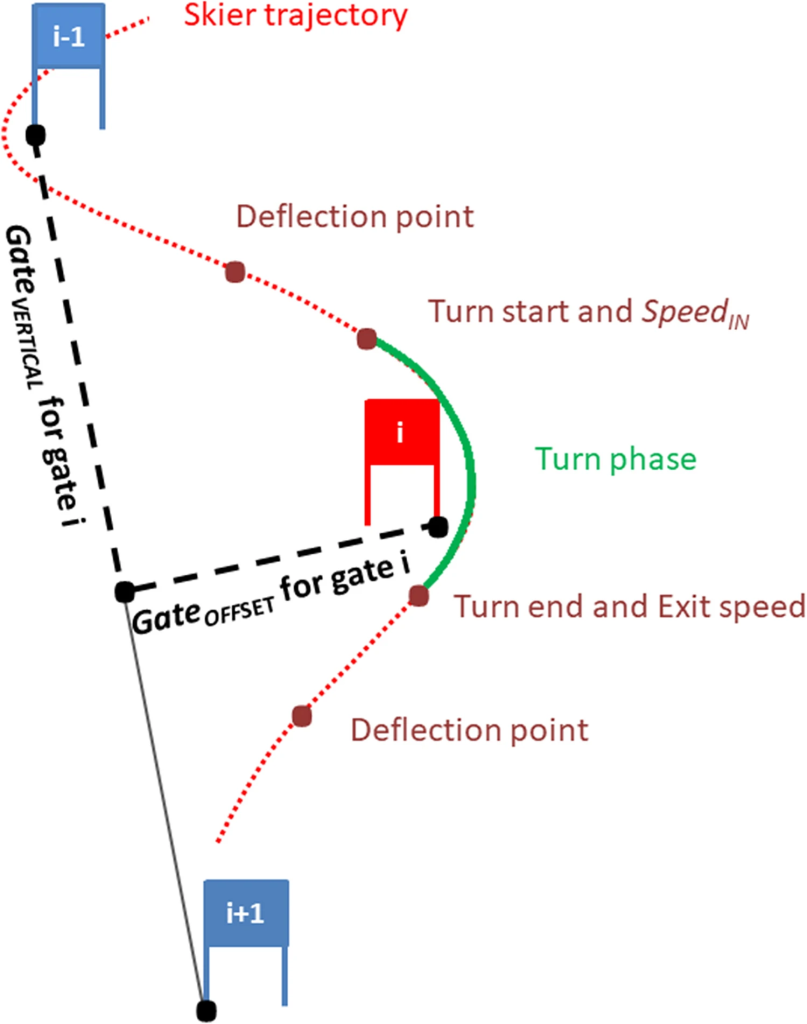 |
私がNutralPointと呼んでいる変曲点を変向点DeflectionPointと呼んでる。このほうが意味がわかりやすいので、これからは、 DeflectionPointと呼ぶことにします。 回転範囲の定義を半径75m以内をターン中としている。 STAでも軌跡の回転半径を計算してみます。開始速度と終了速度を回転範囲の開始終了で定義してます。 |
| 動き 計算 方法 |
スキーヤーメカニクスの計算 競技者のヘルメットに取り付けられたdGNSSアンテナの位置を、二次曲線スプライン関数を用いてフィルタリングしました。質量中心(CoM)の位置をより正確に推定するために,機械的な振り子モデルをアンテナの位置に取り付け,グローバルな位置精度を9±12cmとした。振り子の重心位置のデータから,瞬間的な速度,旋回半径,地面反力とインパルスを時間的に求めた。ターンの開始と終了は,スキーヤーのCoM軌道(水平面に投影)の2つの偏向点間の位相として定義し,CoMのターン半径は75m以下とした。選手がターンに入るときの速度(SpeedIN)は,ゲート通過前にターン半径が75m以下になった時点での瞬間速度と定義した.ゲート通過後、初めて旋回半径が75mを超えた時点での瞬間速度を出口速度とした。旋回中の速度変化(△Speed)は、SpeedINとExit speedの差として計算した。旋回中の最小旋回半径(RadiusMIN)も傷害代用として考慮し,旋回中の最小半径として定義した.最大地面反力(GRFMAX)は、ターン中の瞬間的な地面反力の最大値と定義した24。選手がコース上で周囲に及ぼした努力を測定するために、外力の時間積分としてインパルスを算出した。インパルスは、肉体的努力の持続時間と強度の両方がこの指標に反映されるため、蓄積された疲労の近似値としても機能する可能性がある。疲労の代用としてのインパルスは、ターン時間中の地面反力と空気抵抗(体重単位)の積分として定義され、体重秒(BWs)で表された。 |
アンテナ部にIMUをとりつけて 重心位置の推定に使っている 軌跡は、二次のスプライン補間で軌跡を描いている。 重心位置のデータから旋回半径、地面反力を求めている。 SpeedInを75m半径に入る点 Exit speedを75m半径から出る点Δspeed=SpeedIn-Exit seedRadiusMIN 最小旋回半径GRFMAX 最大地面反力(重心の加速度最大x質量)BWs 地面反力の時間積分を仕事量として積算 これは選手の疲労度の近似値としてみる。Impulse 外力の時間積分全体 |
| 全体 データ 処理 |
統計解析 全4レースのデータをプールし,192回のターンのデータセットを作成した。コース設定と選手の機械的パラメータの中心傾向とばらつきを明らかにするため,平均値と標準偏差(SD)を算出した。コース設定とコース設定の調整,およびそれらがスキーヤーの力学に及ぼす影響の関係を明らかにするため,線形混合効果モデルを構築した(192ターン,SAS 9.4 SoftwareのMIXED手順,Raleigh, USA)).雪の状態が数値化されておらず,各レース地で前走者が異なるため,モデルにはランダム変数「スキーヤーID」(3人の異なる選手)と「スキーヤーID*レースID」を入れた。モデルの予測因子として,以下の変数が含まれていました。モデルの予測変数として,「SpeedIN」,「TerrainINCLINE」,「GateOFFSET」,「GateVERTICAL」を用いた.混合モデルは,各結果変数について実行した。混合モデルは、RadiusMIN、∆Speed、GRFMAX、Impulseの各結果変数について実行されました。異なる結果変数間で比較可能な結果を生成するために、モデルの固定効果を2SDで除算して調整した。この中間段階の計算結果は補足資料に掲載されている。結果をこのようにスケーリングすることで、モデルは「ΔSpeedを2標準偏差分変化させるには、GateVERTICALをどれだけ変化させる必要があるか」という意味で解釈することができる。混合モデルをすべてのターンで再実行し、ターン開始からターン終了までに速度が0.5m/s減少(△速度=-0.5m/s)するために各予測変数(SpeedIN、TerrainINCLINE、GateOFFSET、GateVERTICAL)に必要な調整量を算出した。この予測変数の変更(速度を0.5m/s減少させる)が他の結果変数であるRadiusMIN、GRFMAX、Impulseに与える影響も測定した。 |
ターン毎の平均値とσを算出している https://jp.mathworks.com/help/stats/linear-mixed-effects-models.html 雪の状態が異なるので、モデルに重みをつけている。 モデル構築で使っているパラメータは 予想パラメータは
|
| 結果
1 |
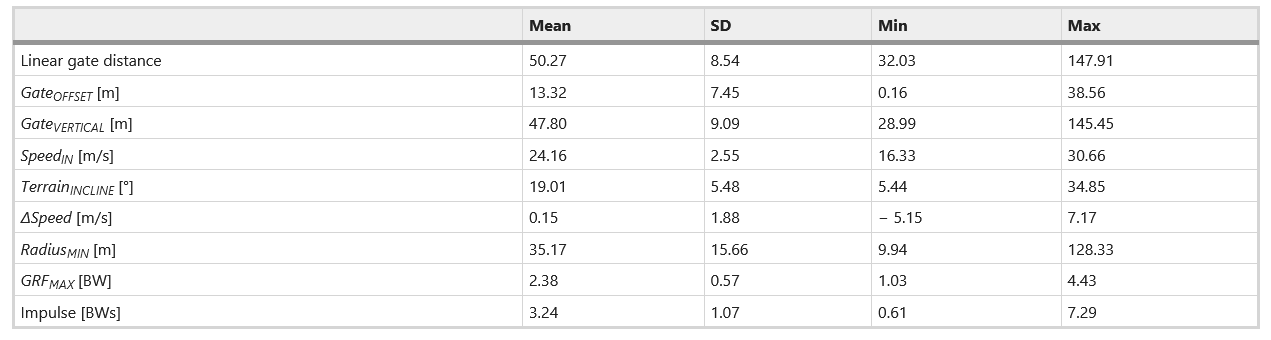
結果 下表1は、混合モデルの予測変数と結果変数の中心傾向、変動性、範囲(平均値、SD値、最小値、最大値)の概要を示したもので、競技種目「Super-G」では、GateOFFSETがGateVERTICALや直線的なゲート距離よりもはるかに高い変動性を持つことが明らかになった。 平均値 SD 最小値 最大値 リニアゲート距離 50.27 8.54 32.03 147.91 ゲートオフセット [m] 13.32 7.45 0.16 38.56 ゲートVERTICAL [m] 47.80 9.09 28.99 145.45 スピードIN [m/s] 24.16 2.55 16.33 30.66 地形インクライン [°] 19.01 5.48 5.44 34.85 ∆Speed [m/s] 0.15 1.88 – 5.15 7.17 半径MIN [m] 35.17 15.66 9.94 128.33 GRF MAX [BW] 2.38 0.57 1.03 4.43 インパルス [BWs] 3.24 1.07 0.61 7.29コース設定,入口速度,地形傾斜の調整が速度低下に及ぼす影響 表2は、コース設定、地形の傾斜、SpeedINの変化が△Speed(旋回時の調整による速度低下)に与える影響を記述した線形混合効果モデルの結果である。すべてのモデル予測因子が速度に有意な影響を与えている。
|
表1 Super-G.の混合モデルにおける予測変数と結果変数の平均値、SD値、最小値と最大値
表2 速度(ΔSpeed)を-0.5m/s減少させるために、各予測子にどのような変化が必要かを示した結果。
| 結果
2 |
コース設定,入口速度,地形傾斜の調整が速度低下に及ぼす影響 下表2は、コース設定、地形の傾斜、SpeedINの変化が△Speed(旋回時の調整による速度低下)に与える影響を記述した線形混合効果モデルの結果である。すべてのモデル予測因子が速度に有意な影響を与えている。∆速度 [m/s] p値 速度を 0.5m/s 低下させるのに必要な m の絶対的変化 速度を 0.5m/s 低下させるのに必要な % の相対的変化 予測値 ゲートオフセット [m] < 0.0001 6.84 51 予測値 ゲートVERTICAL [m] < 0.0001 – 6.31 – 13 予測値 SpeedIN [m/s] < 0.0001 2.2 9 予測値 地形陰線 [°] < 0.0001 – 3.68 – 19ターン全体で0.5m/sの速度低下を実現するためには、GateOFFSETを既存のGateOFFSETの51%、つまり平均6.84m増加させる必要がある。同じ速度低下を実現するためには、GateVERTICALを既存のGateVERTICALの13%である-6.31m短縮する必要がある。さらに、コース設定や地形が一定であっても、スキーヤーが2.2m/sまたは9%高い入口速度(SpeedIN)でターンに入ると、「速度の壁」(=ミスを避けるためにスキーヤーが自発的に速度をコントロールすること)の現象により、ターン中に0.5m/sの速度が失われることになります。また、あるコース設定とSpeedINの場合、3.68°急なTerrainINCLINEは、あるTerrainINCLINEでのターンと比較して、ターンを通して0.5m/sの速度を失うことになる。 |
| 結果3 | コース設定の調整が旋回半径、地面反力、インパルスに与える影響 下表3のデータによると、GateOFFSETを+6.84m(表2)増加させたことで旋回速度(⊿Speed)が-0.5m/s減少した場合、RadiusMINは-6.57m小さくなり、-19%の減少に相当する。対照的に、GateVERTICALが-6.31m短くなったことで旋回時の速度が-0.5m/s低下すると(表2)、RadiusMINの減少量は大幅に小さくなる(絶対値:-1.40m/割合:-4%)。RadiusMIN [m] p value Absolute reduction in RadiusMIN in m as a consequence of speed reduction of 0.5 m/s Relative reduction in RadiusMIN in % as a consequence of speed reduction of 0.5 m/s Predictor GateOFFSET [m] < 0.0001 - 6.57 - 19 Predictor GateVERTICAL [m] 0.0100 - 1.40 - 4 GRFMAX [BW] p value Absolute reduction in GRFMAX in BW as a consequence of speed reduction of 0.5 m/s Relative reduction in GRFMAX in % as a consequence of speed reduction of 0.5 m/s Predictor GateOFFSET [m] < 0.0001 0.13 6 Predictor GateVERTICAL [m] 0.6700 – Impulse [BWs] p value Absolute reduction in impulse in BWs as a consequence of speed reduction of 0.5 m/s Relative reduction in impulse in % as a consequence of speed reduction of 0.5 m/s Predictor GateOFFSET [m] < 0.0001 0.87 27 Predictor GateVERTICAL [m] 0.0100 - 0.07 - 2 さらに,速度を-0.5 m/s下げるためにGateOFFSETを+6.84 m増やすと(表2),GRFMAXは+0.13 BW(つまり+6%)とわずかだが有意に増加する.GateVERTICALを-6.31m短くして速度を-0.5m/sにしてもGRFMAXの増加は見られない。 最後に、GateOFFSETを+6.84m伸ばして速度を-0.5m/sにすると、インパルスは+0.87BW(=+27%)増加する。一方、GateVERTICALを-6.31m短くして速度を-0.5m/sにすると、インパルスは実際には-0.07BW(=-2%)減少する。
|
表3 コース設定の調整により速度を△0.5m/s下げた場合、RadiusMIN、GRFMAX、インパルスにどのような影響があるかを示した結果。
| 考察 | 考察 この研究の主な発見は,旋回中に速度を-0.5 m/s減少させるためにGateOFFSETを増加させると(+ 6.84 m; + 51%),同時にRadiusMINが減少し(- 19%),Impulseが増加し(+ 27%),GRFMAXが増加する(+ 6%)ということである.GateVERTICALを変更して速度を-0.5m/s下げるには、GateOFFSETに比べてはるかに小さな割合の変更が必要である(-6.31、-13%)。さらに,速度を-0.5 m/s下げるためにGateVERTICALを短くすると,RadiusMIN(-4%)とImpulse(-2%)の減少がはるかに小さくなり,GRFMAXの増加はない。 このように,スーパーGレースでは,コース設定の特性,進入速度,地形の傾斜がスピードに大きく影響し,コース設定を直接変更することで予防が可能であることがわかった。GateOFFSETを大きくしても、GateVERTICALを小さくしても、どちらもスピードの低下につながるが、同じスピード低下(-0.5m/s)でも、GateOFFSET(+51%)の方がGateVERTICAl(-13%)よりも、必要なパーセンテージの変化は約4倍大きく、絶対的な変化は同程度である(表2)。先行研究では、この割合の違いがGSでもあることがわかっていたが、GSでは今回のような4倍の違いではなく、2倍の違いでしかなかった(補足資料の表7参照)。しかし、GSでは、今回の研究のように4倍ではなく、2倍の差しかありませんでした。このSuper-GとGSの大きな違いは、スキーと雪の相互作用に関係していると考えられる。Super-Gでは、GSに比べてターンをより大きく刻むことができ、ピボットやスキッドをあまり使わないと考えられる。これは、ダウンヒルやスラロームでは、カービングに比べてスキッディングの方がスキーと雪の摩擦が大きくなるという知見からも裏付けられています。 スラロームやジャイアント・スラロームにおける先行研究の結果と同様に、入口速度が高いほど、ターン中の速度低下(エネルギー散逸)が大きくなった。この知見は、いわゆる「速度の壁」の存在をさらに裏付けるものであり、スキーヤーがミスをしないためには、コース上の特定のポイントでエネルギーを散逸させる(ブレーキで速度をコントロールする)必要があるという考え。しかし、今回の研究では、この現象をSuper-Gアルペンスキーで初めて説明しました。最後に,地形の傾斜もSuper-Gのスピードコントロールに重要な役割を果たしている。今回の研究では,地形の傾斜が-19%(3.68°)減少すると,速度が0.5m/s減少することが示されたが,これは他の競技での過去の観察結果と一致している.しかし,入場速度と地形は,特定のレース会場のコース設定によって間接的にしか変更できないため,操作可能な予防アプローチというよりは,重要な交絡因子として考えなければならない。 本研究の結果、コース設定者はGateOFFSETを大きくするか、GateVERTICALを小さくすることで速度を制御し、低減できることがわかった。しかし、コース設定者がGateOFFSETとGateVERTICALのどちらを調整して速度を制御するかを決定する際には、速度低下に対する割合の違い(GateVERTICALを減少させる方が大きい)だけが重要な要素ではない。本研究では、速度を0.5m/s下げるためにGateOFFSETを大きくすると、最小回転半径の減少、最大地面反力の増加、インパルスの増加などの弊害が生じることがわかった(表3)。これらの要因は、コース設定の変更がスキーヤーの荷重負荷、バランス、疲労に悪影響を及ぼす欠点としてよく知られているので、GSで先に発見されたように、GateOFFSETを増やすよりもGateVERTICALを短くする方が有利であるという結論は、Super-Gではさらに明らかになりました(補足資料の表7参照)。さらに、GSと同様に、スピード系の種目であるSGとDownhillにおいても、コース設定を調整することによるスピード低下の潜在的な効果(今回の研究)は、スキー用具を改造して得られる効果よりもはるかに高いと思われる。今日まで、ウェアによる空気抵抗の増加がスピード競技のスピードを十分に低下させるかどうかは、科学的に調査されていません。パディングを追加したり、空気抵抗係数の高いレーシングスーツの生地を使用したりすると、空気抵抗が増加し、スピードが低下する可能性があります。また、パディングは衝突時の衝撃吸収を向上させる可能性があります。雪の特性もスピードに大きな影響を与える可能性がありますが、特にコースが長く、雪の特性の発生に環境要因が重要な役割を果たすSGやダウンヒルでは、これらはレース主催者の手に委ねられている部分があります。 スーパーGでは、(1)ダウンヒルに比べて平均速度がわずかに低い(-2m/s)ため、衝撃事故の衝撃エネルギーがダウンヒルに比べてわずかに低いこと、(2)コースが技術的に難しいこと、(3)ダウンヒルのように競技前にスキーヤーがコース上でトレーニングを行わないことなどから、怪我の予防は難しい。具体的には、Super-Gのコースは急勾配で、半径の小さいターンが多く、地形の変化がより頻繁で顕著である。地上反力はダウンヒルよりも高く、競技中の物理的な負荷(インパルス)はダウンヒルよりも13%しかありません。また、スーパーGのコースには平均2.3回のジャンプが含まれており(ダウンヒルは4.2回)、ジャンプの長さはダウンヒルに比べて21%、エアタイムは6%しか短縮されていません。そのため、スーパーGのジャンプはダウンヒルと同様に難易度が高く、テイクオフ時に与えられた回転衝動がダウンヒルとほぼ同じようにバランスを崩した回転を引き起こす可能性があるからだ。 ダウンヒルでは、大会前に選手がコースに慣れるために、少なくとも1回はコースでの公式トレーニングに参加することが安全上の要件となっている。Super-Gでは、選手は競技の数時間前にしかコースを点検する機会がないため、スキー戦略を予測し、パフォーマンスと安全性のバランスを取る必要があります。Super-Gで怪我を防ぐことは、選手だけでなく、主催者やコース設定者にとっても難しいことです。ダウンヒルでは、コース設定が毎年同じように保たれているため、主催者は何年もかけてコースを学び、改善していくことができます。一方、スーパーGのコースは、毎年異なるコーチによって設定され、それに合わせて変化していきます。ゆえに、コースの安全性に最終的な責任を持つコースセッターや国際スキー連盟FISのレースディレクターは、競技前にスーパーGのコースの安全性をテストする機会がありません。そのため、コース設定の経験が重要となります。しかし、WCのコーチがスーパーGのトレーニングコースを設定するのは年間約40回に過ぎないため、これを構築するには何年もかかるかもしれません。ほとんどの場合、競技会よりも簡単で短い斜面で行われます。今回の研究結果は、Super-Gの安全なコース設定と適切なスピードコントロールの方法について、コース設定者の理解を深めるのに役立つと思われます。 この研究結果を解釈する際には、いくつかの制限があります。 |
たった0.5m/secを遅くさせるための、研究ですが
結果は出てます。旗門を振るのか、旗門を離すのかで コース設計での参考になると思います。
STA開発で、非常に参考になる論文でした。 ②ターンの入り口を半径で切り取るのも真似します。 ③GateVERTICALを基準に考えるのも真似します。
|
この翻訳はDeepLを使ったそうですが、なかなかよくできてますが、chatGPTと比較してみるのも面白いです。